题目内容
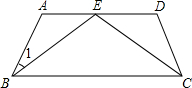
 已知如图,等腰梯形ABCD,AB=CD,BE=CE,求证:AE=DE.
已知如图,等腰梯形ABCD,AB=CD,BE=CE,求证:AE=DE.分析:由等腰梯形ABCD,AB=CD,根据等腰梯形同一底上的两个角相等,可求得∠ABC=∠DCB,又由BE=CE,利用等边对等角的知识,可得∠EBC=∠ECB,继而可证得∠EBA=∠ECD,则可利用SAS证得△EBA≌△ECD,即可证得AE=DE.
解答:证明:∵等腰梯形ABCD,AB=CD,
∴∠ABC=∠DCB,
∵BE=CE,
∴∠EBC=∠ECB,
∴∠EBC-∠ABC=∠ECB-∠DCB,
即∠EBA=∠ECD,
在△EBA和△ECD中,
,
∴△EBA≌△ECD(SAS),
∴AE=DE.
∴∠ABC=∠DCB,
∵BE=CE,
∴∠EBC=∠ECB,
∴∠EBC-∠ABC=∠ECB-∠DCB,
即∠EBA=∠ECD,
在△EBA和△ECD中,
|
∴△EBA≌△ECD(SAS),
∴AE=DE.
点评:此题考查了等腰梯形的性质、等腰三角形的性质以及全等三角形的判定与性质.此题难度不大,解题的关键是掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、已知如图,等腰梯形ABCD中,AD∥BC,AB=DC,E是AD的中点.
22、已知如图,等腰梯形ABCD中,AD∥BC,AB=DC,E是AD的中点. 26、已知如图,等腰梯形锐角等于60°,它的两个底分别为15cm和49cm,求腰长.
26、已知如图,等腰梯形锐角等于60°,它的两个底分别为15cm和49cm,求腰长. 已知如图,等腰梯形ABCD中,AD∥BC,AB=DC,E、F、G、H依次是AB、BC、CD、DA的中点,你认为四边形EFGH会是什么特殊四边形?请证明你的结论.
已知如图,等腰梯形ABCD中,AD∥BC,AB=DC,E、F、G、H依次是AB、BC、CD、DA的中点,你认为四边形EFGH会是什么特殊四边形?请证明你的结论.