题目内容
已知如图，等腰梯形ABCD中，AD∥BC，AB=DC，E是AD的中点．
（1）求证：EB=EC；
（2）若BE⊥EC，∠A=120°，求∠1的度数．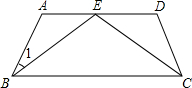
（1）求证：EB=EC；
（2）若BE⊥EC，∠A=120°，求∠1的度数．
（1）证明：∵E是AD的中点，∴AE=DE，
∵四边形ABCD为等腰梯形，∴AB=CD，∠A=∠D，
∴△ABE≌△DCE，∴EB=EC；
（2）∵∠A=120°，∴∠ABC=60°，
∵EB=EC，∴∠EBC=∠ECB，∵BE⊥EC，
∴∠EBC=∠ECB=45°，∴∠1=15°．
∵四边形ABCD为等腰梯形，∴AB=CD，∠A=∠D，
∴△ABE≌△DCE，∴EB=EC；
（2）∵∠A=120°，∴∠ABC=60°，
∵EB=EC，∴∠EBC=∠ECB，∵BE⊥EC，
∴∠EBC=∠ECB=45°，∴∠1=15°．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
22、已知如图，等腰梯形ABCD中，AD∥BC，AB=DC，E是AD的中点．
26、已知如图，等腰梯形锐角等于60°，它的两个底分别为15cm和49cm，求腰长．
已知如图，等腰梯形ABCD中，AD∥BC，AB=DC，E、F、G、H依次是AB、BC、CD、DA的中点，你认为四边形EFGH会是什么特殊四边形？请证明你的结论．
已知如图，等腰梯形ABCD，AB=CD，BE=CE，求证：AE=DE．