Question

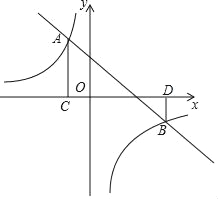
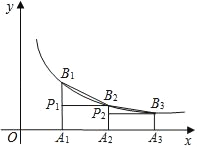
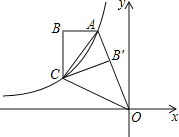
【题目】如图，双曲线y=（x＜0）经过Rt△ABC的两个顶点A，C，∠ABC=90°，AB∥x轴，连接OA，将Rt△ABC沿AC翻折后得到Rt△AB′C，点B′刚好落在线段OA上，连接OC，OC恰好平分OA与x轴负半轴的夹角，若Rt△ABC的面积为2，则k的值为___．

Answer 1

【答案】﹣4．

【解析】

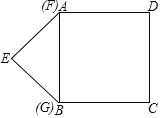
延长BC，与x轴交于点D，可得CD⊥x轴，作AE⊥x轴，如图所示，由折叠的性质得到Rt△ABC≌Rt△AB′C，再由角平分线定理得到BC=B′C=CD=b，AB=m，设A（-a，2b），根据题意求出mb=4，2ab=k，利用反比例函数的性质列出关于k的方程，求出方程的解即可得到k的值．

延长BC，与x轴交于点D，可得CD⊥x轴，作AE⊥x轴，如图所示，

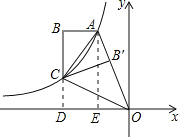
∵Rt△ABC沿AC翻折后得到Rt△AB′C，且Rt△ABC的面积为1，

∴Rt△ABC≌Rt△AB′C，

∵OC平分∠AOD，CD⊥OD，CB′⊥OA，

∴CD=CB′=CB=b，

设AB=m，A（-a，2b），BC=b，则OD=-m-a，

bm=2，即bm=4，

∴S△COD=-k=ODCD=（m+a）b=（mb+ab）=（4-）=2-，

解得：k=-8．

故答案为：-8．