题目内容
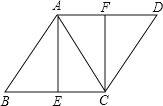
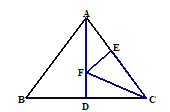
【题目】如图,△ABC中,AB=AC=5,BC=6,AD是BC边上的中线且AD=4,![]() 是AD上的动点,
是AD上的动点,![]() 是AC边上的动点,则
是AC边上的动点,则![]() 的最小值是( ).
的最小值是( ).
A. 6 B. 4 C. ![]() D. 不存在最小值
D. 不存在最小值
【答案】C
【解析】
由已知条件可知,点B和点C关于AD对称,由此可知,CF+EF=BF+EF,因此当点B、E、F三点在同一直线上,且BE⊥AC时,CF+EF的值最小,计算出此时BE的长度即可.
如下图,过点B作BE⊥AC于点E,交AD于点F,
∵AB=AC=5,AD是BC边上的中线,
∴AD⊥BC于点D,
∴点B和点C关于AD对称,
∴CF+EF=BF+EF,
∴当点B、E、F三点在同一直线上,且BE⊥AC时,CF+EF的值最小,
∵BE⊥AC于点E,AD⊥BC于点D,
∴S△ABC=![]() AC·BE=
AC·BE=![]() AD·BC,即
AD·BC,即![]() ,
,
解得:BE=![]() ,
,
∴CF+EF的最小值为:![]() .
.
故选C.


练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目