Question

【题目】如图，四边形ABCD是等腰梯形，∠ABC=60°，若其四边满足长度的众数为5，平均数为 ，上、下底之比为1：2，则BD= ．

Answer 1

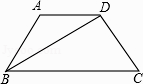
【答案】5
【解析】解：设梯形的四边长为5，5，x，2x，
则 = ，
x=5，
则AB=CD=5，AD=5，BC=10，
∵AB=AD，
∴∠ABD=∠ADB，
∵AD//BC，
∴∠ADB=∠DBC，
∴∠ABD=∠DBC，
∵∠ABC=60°，
∴∠DBC=30°，
∵等腰梯形ABCD，AB=DC，
∴∠C=∠ABC=60°，
∴∠BDC=90°，
∴在Rt△BDC中，由勾股定理得：BD= =5 ，
故答案为：5 ．
设梯形的四边长为5，5，x，2x，根据平均数求出四边长，求出△BDC是直角三角形，根据勾股定理求出即可．