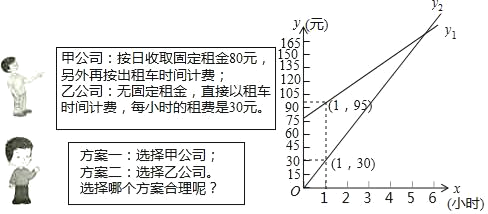
题目内容
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
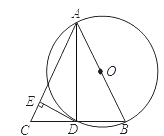
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O半径为5,∠BAC=60°,求DE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)根据垂直平分线的判断方法与性质易得AD是BC的垂直平分线,故可得AB=AC;
(2)连接OD,由平行线的性质,易得OD⊥DE,且DE过圆周上一点D故DE为⊙O的切线;
(3)由AB=AC,∠BAC=60°知△ABC是等边三角形,根据等边三角形的性质,可得AB=BC=10,CD=![]() BC=5;又∠C=60°,借助三角函数的定义,可得答案.
BC=5;又∠C=60°,借助三角函数的定义,可得答案.
试题解析:(1)∵AB是⊙O的直径,
∴∠ADB=90°;
∵BD=CD,
∴AD是BC的垂直平分线.
∴AB=AC.
(2)证明:连接OD,
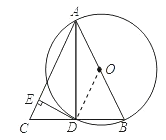
∵点O、D分别是AB、BC的中点,
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE.
∴DE为⊙O的切线.
(3)由AB=AC,∠BAC=60°知△ABC是等边三角形,
∵⊙O的半径为5,
∴AB=BC=10,CD=![]() BC=5.
BC=5.
∵∠C=60°,
∴DE=CDsin60°=![]()

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】某病人每天下午需要测量一次血压,下表是该病人本周星期一至星期五收缩压的变化情况.(“+”表示上升,“-”表示下降)
星期 | 一 | 二 | 三 | 四 | 五 |
收缩压的变化(与前一天比较) | +30 | -20 | +17 | +18 | -20 |
(1)本周三与周一相比较收缩压________了;(填“上升”或“下降”)
(2)通过计算说明本周五收缩压与上周日相比是上升了还是下降了,并求出上升或下降了多少;
(3)如果该病人本周五的收缩压为185,那么他上个周日的收缩压为多少?
【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?