��Ŀ����
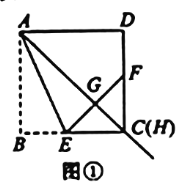
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC����AOC��30������һֱ�����ǰ壨��M��30������ֱ�������ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���

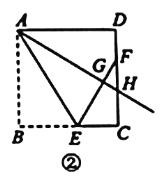
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��5�����ٶ�����ʱ�뷽����תһ�ܣ���ͼ2������t���ON����OC���ϣ���t�����루ֱ��д�������
��2���ڣ�1���������£������ǰ����ת����ͬʱ����OCҲ��O����ÿ��10�����ٶ�����ʱ�뷽����תһ�ܣ���OCת��9��ʱ�����MOC�Ķ�����
��3���ڣ�2���������£����Ǽ����˶�������ʱ����MOC��35������˵�����ɣ�
���𰸡���1��6����2����MON��45�㣻��3�����Ǽ����˶�11���25ʱ����MOC��35�㣮
��������
��1�����ݣ����Ƕȣ��ٶ�![]() ʱ�䡱���м��㣬�������ʱ�䣻
ʱ�䡱���м��㣬�������ʱ�䣻
��2����t��9ʱ������á�AOC�͡�AON��ͨ������ǵIJ����ô𰸣�
��3�����췽����⼴�ɣ�ע���������.
��1��������5t��30�����t��6��
�ʴ�Ϊ6��
��2����t��9ʱ����AOC��30��+9��10�㣽120�㣬��AON��120��+9��5�㣽165�㣬
���ʱ��MON����AOC����AOM��165�㩁120�㣽45�㣮
��3��������˶�t��ʱ����MOC��35�㣮
�����⣺120��+5t����30��+10t����35���30��+10t����120��+5t����35��
���t��11��25��
�����Ǽ����˶�11���25ʱ����MOC��35�㣮