题目内容
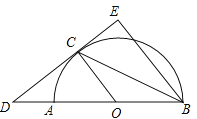
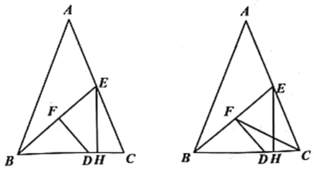
【题目】已知：如图1，△ABC中，AB＝AC，BC＝6，BE为中线，点D为BC边上一点；BD＝2CD，DF⊥BE于点F，EH⊥BC于点H．
(1)CH的长为_____；
(2)求BF·BE的值：
(3)如图2，连接FC，求证：∠EFC＝∠ABC．
【答案】（1）1.5（2）18（3）见解析
【解析】
（1）根据BE是AC边上的中线，可以判断出E点是AC的中点，过A作BC的垂线，垂足为G，可以得出EH∥AG，再根据平行线分线段成比例计算即可.
（2）根据BD和CD的关系计算出CD、BD的长，然后结合第（1）问中CH的长，计算出BH的长，根据三角形相似的判定定理求出
，再根据相似三角形的性质定理列出关于BF，BE的比例关系式，化简求解即可.
（3）过A作 AM∥BC 交BE延长线于 M，根据平行线的性质定理得出相等角，通过三角形全等的判定定理推出
，得出AM的长度，以及BM和BE的关系，然后通过AM，BC，BF，BM的数量关系，列出比例关系式，再结合 
，根据相似三角形的判定定理得出
，从而得出
，然后通过等量代换即可求证
.
解：作AG⊥BC于G，
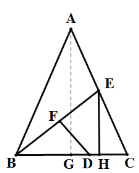
∵AB=AC，BC=6，
∴CG=3，
∵AE=EC，
EH⊥BC，
∴EH∥AG，
（2）
.
，
，
，
，
，
.
（3）过A作 AM∥BC 交BE延长线于 M
，
.
.
，
，
.
，
，
，
，
，
.
练习册系列答案
相关题目
