题目内容
溱湖湿地风景区特色旅游项目:水上游艇. 旅游人员消费后风景区可盈利10元/人,每天消费人员为500人. 为增加盈利,准备提高票价,经调查发现,在其他条件不变的情况下,票价每涨1元,消费人员就减少 20人.
(1)现该项目要保证每天盈利6000元,同时又要旅游者得到实惠,那么票价应涨价多少元?
(2)若单纯从经济角度看,票价涨价多少元,能使该项目获利最多?
(1)现该项目要保证每天盈利6000元,同时又要旅游者得到实惠,那么票价应涨价多少元?
(2)若单纯从经济角度看,票价涨价多少元,能使该项目获利最多?
(1)5元;(2)7.5元
试题分析:(1)设每位消费单价应涨价x元,根据“票价每涨1元,消费人员就减少 20人”即可列方程求解;
(2)设每位消费金额涨价m元,能获利w元,根据“票价每涨1元,消费人员就减少 20人”即可列出w关于m的二次函数,再根据二次函数的性质求解即可.
(1)设每位消费单价应涨价x元,根据题意得
(10+x)(500-20x)=6000
解得
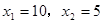
∵该项目要保证每天盈利6000元,同时又要旅游者得到实惠,
∴x=5
答:每位消费单价应涨价5元;
(2)设每位消费金额涨价m元,能获利w元,根据题意得:
W=(10+m)(500-20m)=-20m2+300m+5000
∵a=-200<0,
∴m=
 =7.5元时,获利最多
=7.5元时,获利最多答:单纯从经济角度看,每位消费金额涨价7.5元,能使该项目获利最多.
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
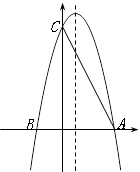
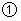 ,在平面直角坐标系中,等腰直角
,在平面直角坐标系中,等腰直角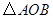 的斜边
的斜边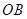 在
在 轴上,顶点
轴上,顶点 的坐标为
的坐标为 ,
,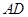 为斜边上的高.抛物线
为斜边上的高.抛物线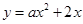 与直线
与直线 交于点
交于点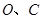 ,点
,点 的横坐标为
的横坐标为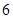 .点
.点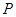 在
在 轴.交射线
轴.交射线 于点
于点 .设点
.设点 ,以
,以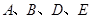 为顶点的四边形的面积为
为顶点的四边形的面积为 .
.
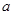 的值;
的值;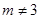 时,求
时,求 ,设直线
,设直线 交射线
交射线 于点
于点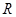 ,交抛物线于点
,交抛物线于点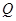 .以
.以 为一边,在
为一边,在 ,其中
,其中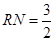 .直接写出矩形
.直接写出矩形
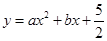 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
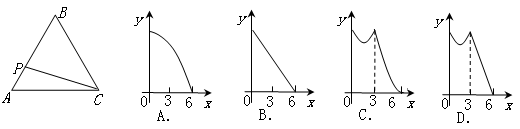

 ;②y=3x-3;③y=x2+3x+3;④y=-(x-3)2+3.
;②y=3x-3;③y=x2+3x+3;④y=-(x-3)2+3.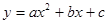 的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x= .
的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x= .