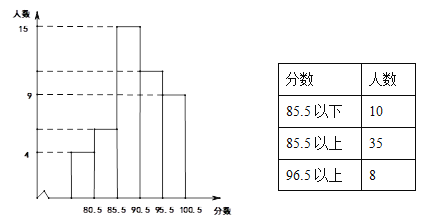
��Ŀ����
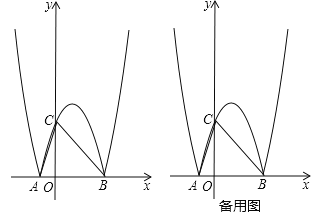
����Ŀ����2017����ʡ��Ǩ�У���25�⣬10�֣���ͼ����ƽ��ֱ������ϵxOy�У�������![]() ��x����A��B���㣨��A�ڵ�B����ࣩ������������λ��x���Ϸ�������M������������λ��x���·�������x�ᷭ�ۣ����ۺ�����������N������N��y���ڵ�C������AC��BC��
��x����A��B���㣨��A�ڵ�B����ࣩ������������λ��x���Ϸ�������M������������λ��x���·�������x�ᷭ�ۣ����ۺ�����������N������N��y���ڵ�C������AC��BC��
��1��������N������������Ӧ�ĺ�������ʽ��
��2������ABC���Բ�İ뾶��
��3����PΪ����M������N�ϵ�һ���㣬��QΪx���ϵ�һ�����㣬���Ե�B��C��P��QΪ������ı�����ƽ���ı��Σ����Q�����꣮
���𰸡���1��![]() ����2��
����2��![]() ����3��Q��4+
����3��Q��4+![]() ��0����4��
��0����4��![]() ��0����5��0����2+
��0����5��0����2+![]() ��0����2��
��0����2��![]() ��0����1��0����
��0����1��0����
��������������1������֪�����߿����A��B���꼰�������꣬���öԳ��Կ����C�����꣬���ô���ϵ�������������N�Ľ���ʽ��
��2�������Բ�Ķ����֪Բ�ļ�Ϊ�߶�BC��AB�Ĵ�ֱƽ���ߵĽ��㣬��ֱ��y=x�������߶Գ���Ľ��㣬��������Բ��Բ�ģ������ù��ɶ�������ð뾶�ij���
��3����Q��x��0������BCΪƽ���ı��εı�ʱ������BQ��PC��BQ=PC���Ӷ�����x��ʾ��P������꣬���������߽���ʽ�ɵõ�x�ķ��̣������Q�����꣬��BCΪƽ���ı��εĶԽ���ʱ����B��C����������ƽ���ı��εĶԳ����ĵ����꣬�Ӷ��ɱ�ʾ��P�����꣬���������߽���ʽ�ɵõ�����x�ķ��̣������P�����꣮
�����������1����![]() �У���y=0�ɵ�x2��2x��3=0�����x=��1��x=3����A����1��0����B��3��0������x=0�ɵ�y=��3����������λ��x���·�������x�ᷭ�ۺ�õ�����N����C��0��3����������N�Ľ���ʽΪ
�У���y=0�ɵ�x2��2x��3=0�����x=��1��x=3����A����1��0����B��3��0������x=0�ɵ�y=��3����������λ��x���·�������x�ᷭ�ۺ�õ�����N����C��0��3����������N�Ľ���ʽΪ![]() ����A��B��C���������ɵ���
����A��B��C���������ɵ��� �������
�������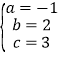 ��������N������������Ӧ�ĺ�������ʽΪ
��������N������������Ӧ�ĺ�������ʽΪ![]() ��
��
��2������ABC���Բ��Բ��ΪM�����MΪ�߶�BC���߶�AB��ֱƽ���ߵĽ��㣬��B��3��0����C��0��3�������߶�BC�Ĵ�ֱƽ���ߵĽ���ʽΪy=x�����߶�AB�Ľ���ʽΪ����N�ĶԳ��ᣬ��x=1����M��1��1������MB=![]() =
=![]() ������ABC���Բ�İ뾶Ϊ
������ABC���Բ�İ뾶Ϊ![]() ��
��
��3����Q��t��0������BQ=|t��3|��
����BCΪƽ���ı��εı�ʱ����ͼ1������BQ��PC����P��������Ϊ3��
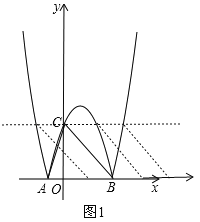
����C����x��ƽ�е�ֱ��������M������N�Ľ��㼴Ϊ��P��x���϶�Ӧ�ļ�Ϊ��Q������P������M��ʱ����![]() �У���y=3�ɽ��x=1+
�У���y=3�ɽ��x=1+![]() ��x=1��
��x=1��![]() ����PC=1+
����PC=1+![]() ��PC=
��PC=![]() ��1��
��1��
��x=1+![]() ʱ����֪��Q�ڵ�B���Ҳ࣬�ɵ�BQ=t��3����t��3=1+
ʱ����֪��Q�ڵ�B���Ҳ࣬�ɵ�BQ=t��3����t��3=1+![]() �����t=4+
�����t=4+![]() ��
��
��x=1��![]() ʱ����֪��Q�ڵ�B����࣬�ɵ�BQ=3��t����3��t=
ʱ����֪��Q�ڵ�B����࣬�ɵ�BQ=3��t����3��t=![]() ��1�����t=4��
��1�����t=4��![]() ����Q��������4+
����Q��������4+![]() ��0����4��
��0����4��![]() ��0����
��0����
����P������N��ʱ����![]() �У���y=3�����x=0����ȥ����x=2����PC=2����ʱQ����B����Ҳ࣬��BQ=t��3����t��3=2�����t=5����Q������Ϊ��5��0����
�У���y=3�����x=0����ȥ����x=2����PC=2����ʱQ����B����Ҳ࣬��BQ=t��3����t��3=2�����t=5����Q������Ϊ��5��0����
����BCΪƽ���ı��εĶԽ���ʱ����B��3��0����C��0��3�������߶�BC���е�Ϊ��![]() ��
��![]() ������P��x��y������x+t=3��y+0=3�����x=3��t��y=3����P��3��t��3��������P������M��ʱ������3=��3��t��2��2��3��t����3�����t=2+
������P��x��y������x+t=3��y+0=3�����x=3��t��y=3����P��3��t��3��������P������M��ʱ������3=��3��t��2��2��3��t����3�����t=2+![]() ��t=2��
��t=2��![]() ����Q��������2+
����Q��������2+![]() ��0����2��
��0����2��![]() ��0����
��0����
����P������N��ʱ������3=����3��t��2+2��3��t��+3�����t=3��Q��B�غϣ���ȥ����t=1����Q������Ϊ��1��0����
���Ͽ�֪Q�������Ϊ��4+![]() ��0����4��
��0����4��![]() ��0����5��0����2+
��0����5��0����2+![]() ��0����2��
��0����2��![]() ��0����1��0����
��0����1��0����

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�����Ŀ������һ���ľ������С���ҵ������̵꣨������꣩�����桢С���������ز�Ѹ������ȫ����С���������к����С����������Ʒ�������Ϣ���±���
��Ʒ | ���� | С�� |
��� | 1kg/�� | 2kg/�� |
�ɱ���Ԫ/���� | 40 | 38 |
�ۼۣ�Ԫ/���� | 60 | 54 |
�����ϱ��ṩ����Ϣ������������⣺
(1)��֪����ǰ����£�С�������������ϱ��й��ĺ����С��3000kg���������4��2��Ԫ������ǰ�����С���������������ֹ��ĺ�����ٴ���
(2)����֮ǰ��������������ƽ���6�µ�10���������£�С�������껹�������ϱ��й��ĺ����С��2000kg�����У����ֹ��ĺ����������������600kg�������������£��������ֹ��ĺ���ζx��kg�����������ֹ��ĺ����С��õ�������Ϊy��Ԫ�������y��x֮��ĺ�����ϵʽ��������������£�С���������������ֹ��ĺ����С�����ٻ�����������Ԫ��