题目内容
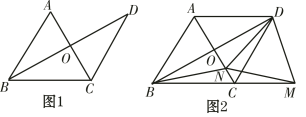
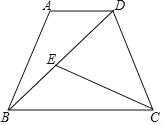
【题目】在梯形ABCD中,AD∥BC,AB=CD,BD=BC,点E在对角线BD上,且∠DCE=∠DBC.
(1)求证:AD=BE;
(2)延长CE交AB于点F,如果CF⊥AB,求证:4EFFC=DEBD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)证明△ABD≌△ECB,可得结论;
(2)连接AC,根据四边形ABCD是等腰梯形,得AC=BD,则BD=BC,由等腰三角形三线合一得:BF=![]() AB,证明△DCE∽△DBC,得CD2=DBDE,再证明△BFE∽△CFB,得BF2=CFEF,由BF2=
AB,证明△DCE∽△DBC,得CD2=DBDE,再证明△BFE∽△CFB,得BF2=CFEF,由BF2=![]() AB2=
AB2=![]() CD2代入可得结论.
CD2代入可得结论.
(1)∵AB=CD,AD∥BC,
∴∠ABC=∠DCB,∠ADB=∠EBC.
∵∠DCE=∠DBC,∠ABC=∠ABD+∠DBC,∠DCB=∠DCE+∠ECB,
∴∠ABD=∠ECB.
在△ABD和△ECB中,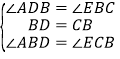 ,
,
∴△ABD≌△ECB(ASA),
∴AD=BE;
(2)连接AC,
∵AD∥BC,AB=CD,
∴四边形ABCD是等腰梯形,
∴AC=BD,
∵BD=BC,
∴AC=BC,
∵CF⊥AB,
∴BF=AF,
∴BF=![]() AB,
AB,
∵∠DCE=∠DBC,
∴△DCE∽△DBC,
∴![]() ,
,
∴CD2=DBDE,
∵∠DCE=∠DBC,
∴∠FBE=∠FCB,
∴△BFE∽△CFB,
∴![]() ,
,
∴BF2=CFEF,
∵BF2=![]() =
=![]() ,
,
∴![]() =CFEF,
=CFEF,
∴![]() DEDB=CFEF,
DEDB=CFEF,
∴4EFFC=DEBD.

【题目】我市某中学学生会在开展“厉行勤俭节约,反对铺张浪费”的主题教育活动中,在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表:根据所给信息,回答下列问题:
选项 | 频数 | 频率 |
A | 36 | m |
B | n | 0.2 |
C | 6 | 0.1 |
D | 6 | 0.1 |
(1)统计表中:m=______;n=______.
(2)该中学有1800名学生晚饭在校就餐,根据调查结果,估计当天晚饭有多少人能够把饭和菜全部吃完?
(3)为了对同学们浪费的行为进行纠正,校学生会从饭和菜都有剩的甲、乙、丙、丁四名同学中任取2位同学进行批评教育,请用列表法或树状图法求恰好抽到甲和丁的概率.