题目内容
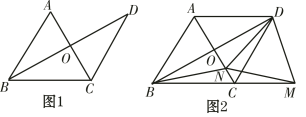
【题目】已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD交AC于点O.
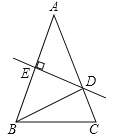
(1)如图1,求证:AC垂直平分BD;
(2)如图2,点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN.求证:NB=NM.
【答案】(1)见解析(2)见解析
【解析】
(1)根据△ABC是等边三角形,确定∠ABC=∠ACB=∠CAB=60°,然后再根据平行线的性质确定∠ACD=∠A=60°=∠ACB,即可解决问题.(2)根据垂直平分线的性质,即垂直平分线上的点到线段两端点的距离相等,确定NB=ND,再根据ND=NM以此解决问题.
解(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠CAB=60°
∵AB//CD,
∴∠ACD=∠A=60°=∠ACB,CD=AB=BC,
∴BO=DO,CO⊥BD,
∴AC垂直平分BD.
(2)证明:∵AC垂直平分BD(已证),
∴NB=ND
又∵ND=NM
∴NB=NM

练习册系列答案
相关题目