题目内容
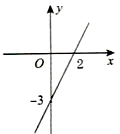 已知一次函数的图象如图.
已知一次函数的图象如图.(1)写出它的函数关系式
(2)根据图象,试直接写出当x<0时,y的取值范围
(3)点P为这条直线上一动点,求线段OP长度的最小值?
分析:(1)根据函数图象与两坐标轴的交点坐标可用待定系数法求出此一次函数的解析式;
(2)根据函数的图象与y轴的交点可直接求出当x<0时,y的取值范围;
(3)过O向直线作垂线即可得到P点,再利用三角形的面积公式即可求解.
(2)根据函数的图象与y轴的交点可直接求出当x<0时,y的取值范围;
(3)过O向直线作垂线即可得到P点,再利用三角形的面积公式即可求解.
解答: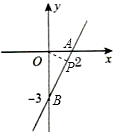 解:(1)由函数的图象可知函数图象与坐标轴的交点为A(2,0)、B(0,-3),
解:(1)由函数的图象可知函数图象与坐标轴的交点为A(2,0)、B(0,-3),
设一次函数的解析式为y=kx+b(k≠0),
把A(2,0)、B(0,-3)代入得,
,
解得,
,故此一次函数的解析式为y=
x-3.
(2)根据函数的图象与y轴的交点可知,当x<0时,y的取值范围y<-3;
(3)过O向直线作垂线,P为垂足,则P点即为所求点,
∵A(2,0)、B(0,-3),
∴OA=2,OB=3,AB=
=
,
∴OA•OB=AB•OP,即2×3=
OP,
∴OP=
.
 解:(1)由函数的图象可知函数图象与坐标轴的交点为A(2,0)、B(0,-3),
解:(1)由函数的图象可知函数图象与坐标轴的交点为A(2,0)、B(0,-3),设一次函数的解析式为y=kx+b(k≠0),
把A(2,0)、B(0,-3)代入得,
|
解得,
|
| 3 |
| 2 |
(2)根据函数的图象与y轴的交点可知,当x<0时,y的取值范围y<-3;
(3)过O向直线作垂线,P为垂足,则P点即为所求点,
∵A(2,0)、B(0,-3),
∴OA=2,OB=3,AB=
| 22+32 |
| 13 |
∴OA•OB=AB•OP,即2×3=
| 13 |
∴OP=
6
| ||
| 13 |
点评:此题比较复杂,涉及到用待定系数法求一次函数的解析式、两点间的距离公式及距离的定义、三角形的面积公式,涉及面较广,但难度适中.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知一次函数 的图象如图所示,则关于
的图象如图所示,则关于 的不等式kx+b>0的解集是( )
的不等式kx+b>0的解集是( )
A. > > | B. < < | C. >1 >1 | D. <1 <1 |
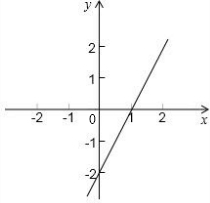 已知一次函数的图象如图,求这个一次函数的解析式.
已知一次函数的图象如图,求这个一次函数的解析式. (2012•翔安区模拟)已知一次函数的图象如图所示,则此一次函数的解析式可以是
(2012•翔安区模拟)已知一次函数的图象如图所示,则此一次函数的解析式可以是 已知一次函数的图象如图所示,写出这个函数的关系式.
已知一次函数的图象如图所示,写出这个函数的关系式.