题目内容
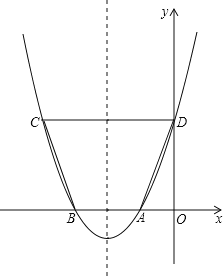
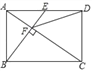
【题目】如图,![]() 内接于半径为
内接于半径为![]() 的半
的半![]() ,
,![]() 为直径,点
为直径,点![]() 是弧
是弧![]() 的中点,连结
的中点,连结![]() 交
交![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,则
,则![]() ______.若点
______.若点![]() 恰好为
恰好为![]() 的中点时,
的中点时,![]() 的长为______.
的长为______.

【答案】![]()
![]()
【解析】
(1)先根据直径所对的圆周角是直角可求出∠ACB=90°,再根据三角形的内角和定理可求出∠BAC+∠ABC=90°,然后根据角平分线的性质可求出∠DAB+∠DBA=45°,最后利用外角的性质即可求出∠MAD的度数;
(2)如图连接AM,先证明△AME∽△BCE,得到![]() 再列代入数值求解即可.
再列代入数值求解即可.
解:(1)∵![]() 为直径,
为直径,
∴∠ACB=90°.
∴∠BAC+∠ABC=90°
∵点![]() 是弧
是弧![]() 的中点,
的中点,
∴∠ABM=∠CBM=![]() ∠ABC.
∠ABC.
∵![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,
∴∠BAD=∠CAD=![]() ∠BAC.
∠BAC.
∴∠DAB+∠DBA=![]() ∠ABC+
∠ABC+![]() ∠BAC=45°.
∠BAC=45°.
∴![]() 45°.
45°.
(2)如图连接AM.
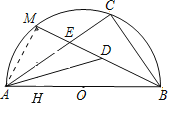
∵AB是直径,
∴∠AMB=90°
∵∠ADM=45°,
∴MA=MD,
∵DM=DB,
∴BM=2AM,设AM=x,则BM=2x,
∵AB=4![]() ,
,
∴x2+4x2=160,
∴x=4![]() (负根已经舍弃),
(负根已经舍弃),
∴AM=4![]() ,BM=8
,BM=8![]() ,
,
∵∠MAE=∠CBM,∠CBM=∠ABM.
∴∠MAE==∠ABM.
∵∠AME=∠AMB=90°,
∴△AME∽△BMA.
∴![]()
∴![]()
∴ME=2![]() .
.
故答案为:(1). ![]() (2).
(2). ![]() .
.

 学练快车道口算心算速算天天练系列答案
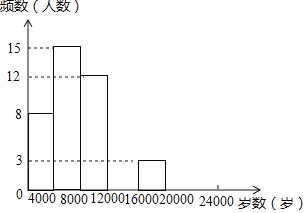
学练快车道口算心算速算天天练系列答案【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.