题目内容
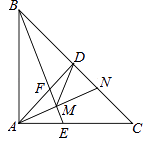
【题目】已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.
(1)若∠ACB=∠CDB=90°,求证:∠CFE=∠CEF;
(2)若∠ACB=∠CDB=m(0°<m<180°). ①求∠CEF﹣∠CFE的值(用含m的代数式表示);
②是否存在m,使∠CEF小于∠CFE,如果存在,求出m的范围,如果不存在,请说明理由.
【答案】
(1)解:∵∠ACB=∠CDB=90°,
∴∠B=90°﹣∠DCB,∠ACD=90°﹣∠DCB,
∴∠B=∠ACD.
∵AE平分∠CAB,
∴∠CFE=∠ACD+ ![]() ∠CAB,∠CEF=∠B+
∠CAB,∠CEF=∠B+ ![]() ∠CAB,
∠CAB,
∴∠CFE=∠CEF
(2)解:①∵∠CFE=∠ACD+ ![]() ∠CAB,∠CEF=∠B+
∠CAB,∠CEF=∠B+ ![]() ∠CAB,
∠CAB,
∴∠CFE﹣∠CEF=∠B﹣∠ACD.
∵∠B=180°﹣m﹣∠DCB,∠ACD=m﹣∠DCB,
∴∠CEF﹣∠CFE=(180°﹣m﹣∠DCB)﹣(m﹣∠DCB)=180°﹣2m;
②存在.
∵要使∠CEF小于∠CFE,则∠CEF﹣∠CFE<0,
∴180°﹣2m<0,解得m>90°,
∴当90°<m<180°时,∠CEF的值小于∠CFE
【解析】(1)先根据∠ACB=∠CDB=90°得出∠B=90°﹣∠DCB,∠ACD=90°﹣∠DCB,再由AE平分∠CAB即可得出结论;(2)①根据三角形外角的性质可得出∠CFE=∠ACD+ ![]() ∠CAB,∠CEF=∠B+
∠CAB,∠CEF=∠B+ ![]() ∠CAB,故∠CFE﹣∠CEF=∠B﹣∠ACD,再由∠B=180°﹣m﹣∠DCB,∠ACD=m﹣∠DCB即可得出结论;②根据∠CEF小于∠CFE可知∠CEF﹣∠CFE<0,故180°﹣2m<0,进而可得出结论.
∠CAB,故∠CFE﹣∠CEF=∠B﹣∠ACD,再由∠B=180°﹣m﹣∠DCB,∠ACD=m﹣∠DCB即可得出结论;②根据∠CEF小于∠CFE可知∠CEF﹣∠CFE<0,故180°﹣2m<0,进而可得出结论.
【考点精析】利用三角形的内角和外角对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案