题目内容
【题目】如图,拦水坝的横断面为梯形ABCD,坝顶宽AD=5米,斜坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
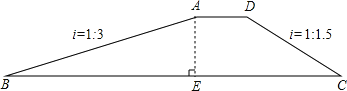
(1)求斜坡AB的长;
(2)求拦水坝的横断面梯形ABCD的周长.(注意:本题中的计算过程和结果均保留根号)
【答案】(1)斜坡AB的长为6![]() m;(2)拦水坝的横断面梯形ABCD的周长为(37+6
m;(2)拦水坝的横断面梯形ABCD的周长为(37+6![]() +3
+3![]() )m.
)m.
【解析】试题分析:(1)已知AE=6m,再结合斜坡AB的坡度可以求出BE、AB的长度;(2)过点D作DF⊥BC于F,可得四边形AEFD是矩形,可得EF=5,DF=6,结合斜坡CD的坡度可以求出CF、CD的长度,进而求出梯形ABCD的周长.
试题解析:
解:(1)∵![]() =i=
=i=![]() ,AE=6m,
,AE=6m,
∴BE=3AE=18m,在Rt△ABE中,根据勾股定理得:AB=![]() =6
=6![]() m,
m,
答:斜坡AB的长为6![]() m;
m;
(2)过点D作DF⊥BC于F,可得四边形AEFD是矩形,
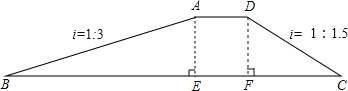
∴EF=AD,∵AD=5m,∴EF=5m,
∵![]() =i=
=i=![]() ,DF=AE=6m,
,DF=AE=6m,
∴CF=![]() DF=9m,
DF=9m,
∴BC=BE+EF+CF=18+5+9=32m,
在Rt△DCF中,根据勾股定理得:
DC=![]() =3
=3![]() m,
m,
∴梯形ABCD的周长为:AB+BC+CD+DA=6![]() +32+3
+32+3![]() +5=(37+6
+5=(37+6![]() +3
+3![]() )m.
)m.
答:拦水坝的横断面梯形ABCD的周长为(37+6![]() +3
+3![]() )m.
)m.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17 20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组 | 划记 | 频数 |
12≤x<17 |
| 3 |
17≤x<22 |
| 10 |
22≤x<27 |
| 5 |
27≤x<32 |
| 2 |

(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.