题目内容
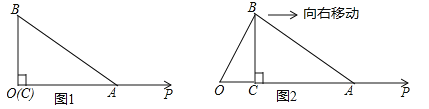
【题目】如图1,Rt△ABC中,∠ACB=90.,直角边AC在射线OP上,直角顶点C与射线端点0重合,AC=b,BC=a,且满足![]() .
.
(1)求a,b的值;
(2)如图2,向右匀速移动Rt△ABC,在移动的过程中Rt△ABC的直角边AC在射线OP上匀速向右运动,移动的速度为1个单位/秒,移动的时间为t秒,连接OB.
①若△OAB为等腰三角形,求t的值;
②Rt△ABC在移动的过程中,能否使△OAB为直角三角形?若能,求出t的值:若不能,说明理由.
【答案】(1)a=3,b=4(2)①t=4或t=1;②能.t=![]() .
.
【解析】
(1)根据两个非负数的和为零则每一个数都为零,得出b-4=0 ,a-3=0 ,求解即可得出a,b的值;
(2)①首先根据勾股定理算出AB的长及用含t的式子表示出OA,OB2,然后分三类讨论:当OB=AB时;当AB=OA时;当OB=OA时;一一列出方程求解即可得出t的值;②能.由于t>0,点C在OP上,∠ACB = 90![]() ,故只能是∠OBA=90°,根据勾股定理得出关于t的方程求出t的值即可.
,故只能是∠OBA=90°,根据勾股定理得出关于t的方程求出t的值即可.
(1)解:∵![]() ,
,![]() ,足
,足![]() ,
,
∴![]() ,
,![]()
∴a=3,b=4
(2)解:①∵AC=4,BC=3,
∴AB=![]() =5,
=5,
∵OC=t
∴OB2=t2+32=t2+9,OA=t+4,
当OB=AB时,t2+9=25,解得t=4或t=﹣4(舍去);
当AB=OA时,5=t+4,解得t=1;
当OB=OA时,t2+9=(t+4)2,解得t=-![]() (舍去).
(舍去).
综上所述,t=4或t=1;
②能.
∵t>0,点C在OP上,∠ACB![]()
∴只能是∠OBA=90°,
∴OB2+AB2=OA2,即t2+9+25=(t+4)2,解得t=![]() .
.
∴Rt△ABC在移动的过程中,能使△OAB为直角三角形,此时t=![]() .
.

练习册系列答案
相关题目