题目内容
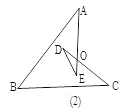
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.
求证:AM=AN.

【答案】证明见解析
【解析】证明:∵△AEB由△ADC旋转而得,∴△AEB≌△ADC。∴∠EAB=∠CAD,∠EBA=∠C。
∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∠ABC=∠C。
∴∠EAB=∠DAB,∠EBA=∠DBA。
∵∠EBM=∠DBN,∴∠MBA=∠NBA。
又∵AB=AB,∴△AMB≌△ANB(ASA)。∴AM=AN。
根据旋转的性质可得△AEB≌△ADC,根据全等三角形对应角相等可得∠EAB=∠CAD,∠EBA=∠C,结合等腰三角形三线合一的性质即可推出∠EAB=∠DAB,∠EBA=∠DBA,从而推出∠MBA=∠NBA,然后根据“角边角”证明△AMB≌△ANB,根据全等三角形对应边相等即可得证。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目