题目内容
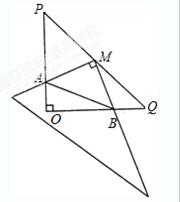
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点,连接BG、CG、PG。

(1)△ABP以点B为旋转中心旋转了 度;
(2)求出PG的长度;(3)以点G为圆心,r为半径作⊙G:
①当半径r满足 时,⊙G与边PC只有一个交点;
②当半径r满足 时,⊙G与边PC有两个交点;
③当半径r满足 时,⊙G与边PC没有交点。

(1)△ABP以点B为旋转中心旋转了 度;
(2)求出PG的长度;(3)以点G为圆心,r为半径作⊙G:
①当半径r满足 时,⊙G与边PC只有一个交点;
②当半径r满足 时,⊙G与边PC有两个交点;
③当半径r满足 时,⊙G与边PC没有交点。
(1)90;(2)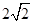 ;(3)
;(3)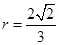 ,
, <r<1;r>
<r<1;r>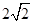 .
.
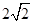 ;(3)
;(3)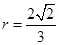 ,
, <r<1;r>
<r<1;r>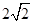 .
.试题分析:(1)根据题意知∠ABC=90°,将△ABP沿顺时针方向旋转,使点A与点C重合时,旋转角为∠ABC=90°;
(2)连接PG,证明△BPG为等腰直角三角形,BP=BG=2,由勾股定理可求PG;
(3)由旋转的性质可知CG=AP=1,已知PC=3,由(2)可知PG,利用勾股定理的逆定理,判断△PGC为直角三角形.利用面积法求出点G到PC的距离,即可解答.
试题解析:(1)旋转后的△BCG如图所示,旋转角为∠ABC=90°;
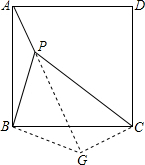
(2)连接PG,由旋转的性质可知BP=BG,∠PBG=∠ABC=90°,
∴△BPG为等腰直角三角形,
又BP=BG=2,
∴PG=
 ;
;(3)(3)由旋转的性质可知CG=AP=1,已知PC=3,
由(2)可知PG=
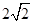 ,
,∵PG2+CG2=(
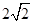 )2+12=9,PC2=9,
)2+12=9,PC2=9,∴PG2+CG2=PC2,
∴△PGC为直角三角形.
过G作GE⊥PC,垂足为E
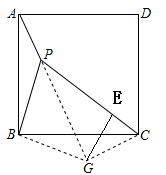
∵
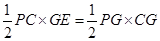
∴
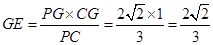 .
.∴当
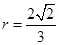 时,⊙G与边PC只有一个交点;当
时,⊙G与边PC只有一个交点;当 <r<1时,⊙G与边PC有两个交点;当r>
<r<1时,⊙G与边PC有两个交点;当r>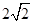 时,⊙G与边PC没 有交点。
时,⊙G与边PC没 有交点。考点: 1.旋转的性质;2.勾股定理;3.勾股定理的逆定理;4.正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
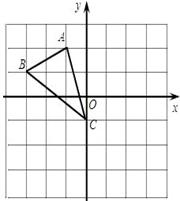
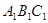 ,则A点的对应点
,则A点的对应点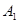 的坐标是 ;
的坐标是 ;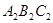 ,则A点对应点
,则A点对应点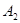 的坐标是 。
的坐标是 。