题目内容
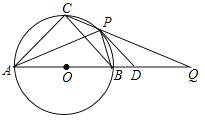
【题目】如图,等腰△ABC三个顶点在⊙O上,直径AB=12,P为弧BC上任意一点(不与B,C重合),直线CP交AB延长线与点Q,2∠PAB+∠PDA=90°,下列结论:①若∠PAB=30°,则弧BP的长为![]() ;②若PD//BC,则AP平分∠CAB;③若PB=BD,则
;②若PD//BC,则AP平分∠CAB;③若PB=BD,则![]() ,④无论点P在弧
,④无论点P在弧![]() 上的位置如何变化,CP·CQ为定值. 正确的是___________.
上的位置如何变化,CP·CQ为定值. 正确的是___________.
【答案】②③④.
【解析】试题解析:如图,连接OP,

∵AO=OP,∠PAB=30°,
∴∠POB=60°,
∵AB=12,
∴OB=6,
∴弧![]() 的长为
的长为![]() =2π,故①错误;
=2π,故①错误;
∵PD是⊙O的切线,
∴OP⊥PD,
∵PD∥BC,
∴OP⊥BC,
∴![]() =
=![]() ,
,
∴∠PAC=∠PAB,
∴AP平分∠CAB,故②正确;
若PB=BD,则∠BPD=∠BDP,
∵OP⊥PD,
∴∠BPD+∠BPO=∠BDP+∠BOP,
∴∠BOP=∠BPO,
∴BP=BO=PO=6,即△BOP是等边三角形,
∴PD=![]() OP=6
OP=6![]() ,故③正确;
,故③正确;
∵AC=BC,
∴∠BAC=∠ABC,
又∵∠ABC=∠APC,
∴∠APC=∠BAC,
又∵∠ACP=∠QCA,
∴△ACP∽△QCA,
∴![]() ,即CPCQ=CA2(定值),故④正确;
,即CPCQ=CA2(定值),故④正确;
故答案为:②③④.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目