题目内容
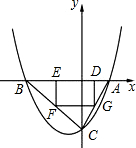
如图,已知抛物线P:y=ax
2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
| X |
… |
-3 |
-2 |
1 |
2 |
… |
| y |
… |
- |
-4 |
- |
0 |
… |
(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k•DF,若点M不在抛物线P上,求k的取值范围;
若因为时间不够等方面的原因,经过探索、思考仍无法圆满解答本题,请不要轻易放弃,试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同,完全正确解答只能得到5分):
(2)若点D的坐标为(1,0),求矩形DEFG的面积.
分析:(1)可任选三组坐标,用待定系数法即可求出抛物线P的解析式.然后根据抛物线P的解析式即可得出A、B、C三点的坐标;
(2)求矩形的面积需知道矩形的长和宽,可先在直角三角形AOC中,根据AD,OA,DG,CD的比例关系式,用m表示出DG的长,同理可在直角三角形BCO中表示出OE的长,进而可根据ED=EO+OD得出ED的长,然后由矩形的面积公式即可得出S与m的函数关系式;
(3)根据(2)的函数关系式即可得出S的最大值及对应的m的值.进而可得出D,E,F,G的坐标.如果设DF的延长线交抛物线于N点,那么可先求出FN与DF的比例关系.如果过N作x轴的垂线设垂足为H,那么我们可得出EF:DF=DF:DN,而EF,DF均为F,N点的纵坐标的绝对值,因此要先求出N点的纵坐标,可先根据D、F的坐标求出直线DF的解析式,然后联立直线DF的解析式与抛物线P的解析式求出N点的坐标,然后根据上述比例关系求出FN、DF的比例关系,如果求出此时FN=k1DF,那么由于M不在抛物线上,因此k的取值范围就是k>0,且k≠k1.
若选(2)可参照上面(2)的求解过程进行计算.
解答: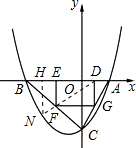
解:(1)解法一:设y=ax
2+bx+c(a≠0),
任取x,y的三组值代入,
| | 4a-2b+c=-4 | | a+b+c=- | | 4a+2b+c=0 |
| |
,
解得
,
∴解析式为
y=x2+x-4,
令y=0,求出x
1=-4,x
2=2;
令x=0,得y=-4,
∴A、B、C三点的坐标分别是A(2,0),B(-4,0),C(0,-4).
(2)由题意,
=,
而AO=2,OC=4,AD=2-m,
故DG=4-2m,
又
=,EF=DG,得BE=4-2m,
∴DE=3m,
∴S
DEFG=DG•DE=(4-2m)3m=12m-6m
2(0<m<2).
注:也可通过解Rt△BOC及Rt△AOC,或依据△BOC是等腰直角三角形建立关系求解.
(3)∵S
DEFG=-6m
2+12m=-6(m-1)
2+6,(0<m<2),
∴m=1时,矩形的面积最大,且最大面积是6.
当矩形面积最大时,其顶点为D(1,0),G(1,-2),F(-2,-2),E(-2,0),
设直线DF的解析式为y=kx+b,易知,k=
,b=-
,
∴
y=x-,
又可求得抛物线P的解析式为:
y=x2+x-4,
令
x-=
x2+x-4,可求出x=
.
设射线DF与抛物线P相交于点N,则N的横坐标为
,过N作x轴的垂线交x轴于H,有
==
=
,
点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是
k≠
且k>0.
若选择另一问题:
(2)∵
=,而AD=1,AO=2,OC=4,则DG=2,
又∵
=,而AB=6,CP=2,OC=4,则FG=3,
∴S
DEFG=DG•FG=6.
点评:本题着重考查了二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.考查学生数形结合的数学思想方法.
练习册系列答案
相关题目
 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下: 解:(1)解法一:设y=ax2+bx+c(a≠0),
解:(1)解法一:设y=ax2+bx+c(a≠0), 解:(1)解法一:设y=ax2+bx+c(a≠0),
解:(1)解法一:设y=ax2+bx+c(a≠0),
 每课必练系列答案
每课必练系列答案 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;