题目内容
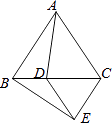
【题目】把两个含有45°角的直角三角板如图放置，点D在AC上，连接AE、BD，试判断AE与BD的关系，并说明理由．
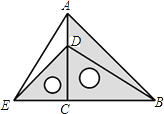
【答案】BF⊥AE，理由详见解析.
【解析】BD=AE ,BD⊥AE.延长BD交AE于F ,证△BCD≌△ACE,可得BD=AE ,BD⊥AE .
∵CE=CD，CA=CB，∠ACE=∠BCD=90°，∴△BCD≌△ACE，∴BD=AE，∠CBD=∠CAE，∵∠CAE+∠AEC=90°，∴∠CBD+∠AEC=90°，∴∠BFE=90°，即BD⊥AE.
【题型】解答题
【结束】
24
【题目】在△ABC中，已知∠B=50°，∠C=60°，AE⊥BC于E，AD平分∠BAC；求：∠DAE的度数．
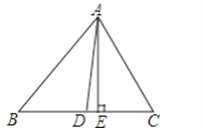
【答案】∠DAE=5°．
【解析】试题分析：根据三角形内角和定理求出∠BAC的度数，再根据角平分线的定义求得∠CAD的度数；在△AEC中，求出∠CAE的度数，从而可得∠DAE的度数．
试题解析：
∵在△ABC中，∠B=50°，∠C=60°，
∴∠BAC=180°﹣50°﹣60°=70°．
∵AD平分∠BAC，
∴∠CAD=
∠BAC=35°．
∵AE⊥BC于E，
∴∠CAE=90°﹣60°=30°，
∴∠DAE=∠CAD﹣∠CAE=35°﹣30°=5°．
练习册系列答案
相关题目
