题目内容
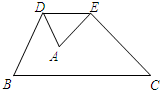
 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=| 1 |
| 2 |
| 1 |
| 2 |
分析:根据折叠得到DE垂直平分AF,再根据对角线互相垂直的四边形的面积等于两条对角线的乘积的一半即可证明③,根据三角形的外角的性质即可证明④.
解答:解:①要使EF∥AB且EF=
AB,则需EF是△ABC的中位线,根据折叠得AE=EF,显然本选项不一定成立;
②要使∠BAF=∠CAF,则需AD=AE,显然本选项不一定成立;
③根据折叠得到DE垂直平分AF,故本选项正确;
④根据三角形的外角的性质,得∠BDF=∠DAF+∠AFD,∠CEF=∠EAF+∠AFE,又∠BAC=∠DFE,则∠BDF+∠FEC=2∠BAC,故本选项成立.
故答案为③④.
| 1 |
| 2 |
②要使∠BAF=∠CAF,则需AD=AE,显然本选项不一定成立;
③根据折叠得到DE垂直平分AF,故本选项正确;
④根据三角形的外角的性质,得∠BDF=∠DAF+∠AFD,∠CEF=∠EAF+∠AFE,又∠BAC=∠DFE,则∠BDF+∠FEC=2∠BAC,故本选项成立.
故答案为③④.
点评:此题综合考查了折叠的性质、对角线互相垂直的四边形的面积等于两条对角线的乘积的一半、三角形的外角的性质.

练习册系列答案
相关题目
 如图,将△ABC沿DE翻折,折痕DE∥BC,若
如图,将△ABC沿DE翻折,折痕DE∥BC,若| AD |
| BD |
| 1 |
| 2 |
| A、1.8 | B、2 | C、2.5 | D、3 |
 (2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=
(2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=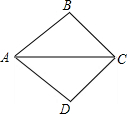 如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( )
如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( ) 如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )
如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )