题目内容
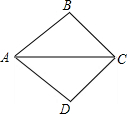 如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( )
如图,将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,则下列结论正确的是( )分析:根据折叠的性质,结合各选项所给的结论一一分析即可得出答案.
解答:解:∵将△ABC沿AC所在的直线翻折得到△ADC,且顶点B的对应顶点是D,
∴△ABC≌△ADC,
∴AB=AD,∠ABC=∠ADC,∠BAC=∠DAC,
∴选项A、C、D错误,选项B正确.
故选B.
∴△ABC≌△ADC,
∴AB=AD,∠ABC=∠ADC,∠BAC=∠DAC,
∴选项A、C、D错误,选项B正确.
故选B.
点评:本题考查了翻折变换(折叠问题),翻折变换实质上就是轴对称变换.熟练掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
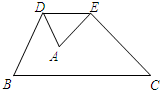 如图,将△ABC沿DE翻折,折痕DE∥BC,若
如图,将△ABC沿DE翻折,折痕DE∥BC,若| AD |
| BD |
| 1 |
| 2 |
| A、1.8 | B、2 | C、2.5 | D、3 |
 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论正确的有( )
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论正确的有( ) (2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=
(2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC= 如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )
如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )