题目内容
如图,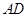 是
是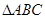 的角平分线, 延长
的角平分线, 延长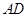 交
交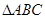 的外接圆
的外接圆 于点
于点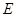 ,过
,过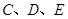 三点的圆
三点的圆 交
交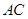 的延长线于点
的延长线于点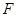 ,连结
,连结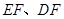 .
.
(1)求证: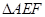 ∽
∽ ;
;
(2) 若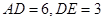 , 求
, 求 的长;
的长;
(3) 若 ∥
∥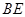 , 试判断
, 试判断 的形状,并说明理由.
的形状,并说明理由.
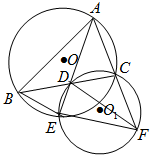
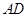 是
是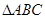 的角平分线, 延长
的角平分线, 延长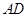 交
交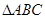 的外接圆
的外接圆 于点
于点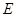 ,过
,过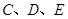 三点的圆
三点的圆 交
交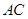 的延长线于点
的延长线于点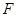 ,连结
,连结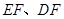 .
.(1)求证:
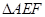 ∽
∽ ;
;(2) 若
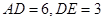 , 求
, 求 的长;
的长;(3) 若
 ∥
∥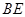 , 试判断
, 试判断 的形状,并说明理由.
的形状,并说明理由.
(1)证明:连结两圆的相交弦
在圆 中,
中,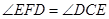 ,
,
在圆 中,
中,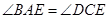 ,
,
∴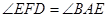 ,
,
又因为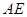 是
是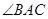 角平分线,得∠BAE=∠CAE,
角平分线,得∠BAE=∠CAE,
∴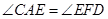 ,
,
∵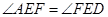 ,
,
∴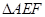 ∽
∽ .
.
(2)∵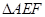 ∽
∽ ,
,
∴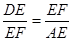 ,
,
∴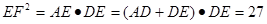 ,
,
∴ .
.
(3)证明:根据同弧上的圆周角相等,
得到: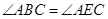 ,
,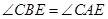 ,
,
∴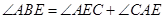 ,
,
∵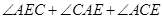 =180°,
=180°,
∴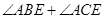 =180°,
=180°,
又 =180,
=180,
∴ .
.
∵ ∥
∥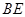 ,
,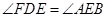 ,
,
又∵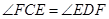 ,
,
∴∠AEB =∠ABE ,
∴ 为等腰三角形.
为等腰三角形.

在圆
 中,
中,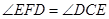 ,
,在圆
 中,
中,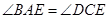 ,
,∴
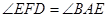 ,
,又因为
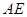 是
是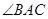 角平分线,得∠BAE=∠CAE,
角平分线,得∠BAE=∠CAE, ∴
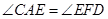 ,
,∵
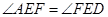 ,
,∴
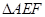 ∽
∽ .
. (2)∵
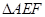 ∽
∽ ,
,∴
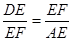 ,
, ∴
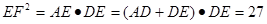 ,
,∴
 .
. (3)证明:根据同弧上的圆周角相等,
得到:
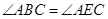 ,
,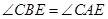 ,
,∴
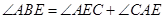 ,
,∵
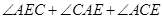 =180°,
=180°,∴
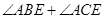 =180°,
=180°,又
 =180,
=180,∴
 .
. ∵
 ∥
∥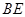 ,
,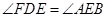 ,
,又∵
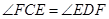 ,
,∴∠AEB =∠ABE ,
∴
 为等腰三角形.
为等腰三角形.(1)可通过证两组对应角相等来证两三角形相似.
(2)根据(1)中得出的相似三角形即可得出AE,DE,EF这三条线段的比例关系,有了AD,DE的长,即可求出EF的值.
(3)可通过证角的关系来得出三角形的形状.
(2)根据(1)中得出的相似三角形即可得出AE,DE,EF这三条线段的比例关系,有了AD,DE的长,即可求出EF的值.
(3)可通过证角的关系来得出三角形的形状.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
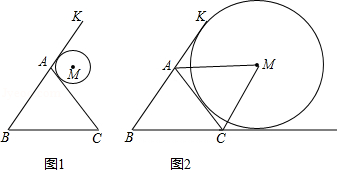
 的值.
的值.
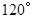 的扇形,则该圆锥的底面半径等于( ).
的扇形,则该圆锥的底面半径等于( ).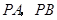 是
是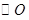 的两条切线,
的两条切线,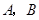 分别为切点,
分别为切点,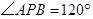 ,
,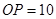 厘米,则弦
厘米,则弦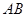 的长为( )
的长为( )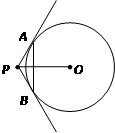
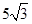 厘米
厘米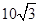 厘米
厘米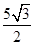 厘米
厘米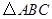 的边长为
的边长为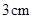 ,边长为
,边长为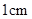 的正
的正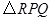 的顶点
的顶点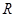 与点
与点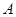 重合,点
重合,点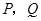 分别在
分别在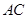 ,
,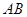 上,将
上,将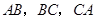 顺时针连续翻转(如图所示),直至点
顺时针连续翻转(如图所示),直至点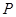 第一次回到原来的位置,则点
第一次回到原来的位置,则点 (结果保留
(结果保留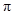 )
)

 于
于 ,若
,若 ,则
,则 .
.