题目内容
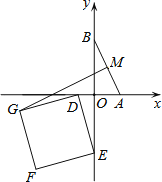
【题目】在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为_____.
【答案】10+5![]()
【解析】
取DE的中点N,连结ON、NG、OM.根据勾股定理可得![]() .在点M与G之间总有MG≤MO+ON+NG(如图1),M、O、N、G四点共线,此时等号成立(如图2).可得线段MG的最大值.
.在点M与G之间总有MG≤MO+ON+NG(如图1),M、O、N、G四点共线,此时等号成立(如图2).可得线段MG的最大值.
如图1,取DE的中点N,连结ON、NG、OM.
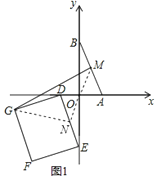
∵∠AOB=90°,
∴OM=![]() AB=5.
AB=5.
同理ON=5.
∵正方形DGFE,N为DE中点,DE=10,
∴![]() .
.
在点M与G之间总有MG≤MO+ON+NG(如图1),
如图2,由于∠DNG的大小为定值,只要∠DON=![]() ∠DNG,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立,
∠DNG,且M、N关于点O中心对称时,M、O、N、G四点共线,此时等号成立,
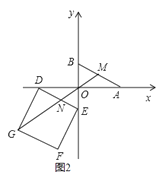
∴线段MG取最大值10+5![]() .
.
故答案为:10+5![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目