题目内容
【题目】如图所示,王刚同学所在的学习小组欲测量校园里一棵大树的高度,他们选王刚作为观测者,并在王刚与大树之间的地面上直立一根高为2m的标杆CD,然后,王刚开始调整自己的位置,当他看到标杆的顶端C与树的顶端E重合时,就在该位置停止不动,这时其他同学通过测量,发现王刚的脚离标杆底部的距离为1m,离大树底部的距离为9m,王刚的眼离地面的高度AB为1.5m,那么大树EF的高为多少?

【答案】大树EF的高为6m.
【解析】
作AH⊥EF于H,AH交CD于G点,利用CG∥EH判断△ACG∽△AEH,然后利用相似比计算出EH,从而得到EF的长.
解:作AH⊥EF于H,AH交CD于G点,如图,
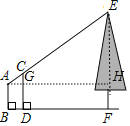
易得BD=1,BF=9,四边形ABDG和四边形ABFH均为矩形
∴DG=HF=AB=1.5,AG=BD=1,
∴CG=CD﹣DG=2﹣1.5=0.5,
∵CG∥EH,
∴△ACG∽△AEH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得EH=4.5,
,解得EH=4.5,
∴EF=EH+FH=4.5+1.5=6(m),
答:大树EF的高为6m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目