题目内容
 (1)解方程:
(1)解方程:| x-3 |
| x-2 |
| 3 |
| 2-x |
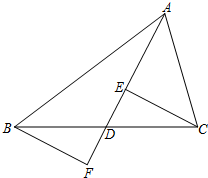
(2)如图,分别过点C、B作△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F.求证:BF=CE.
分析:(1)首先找出最简公分母,再去分母整理,解出分式方程,注意检验;
(2)根据已知得出∠DEC=∠DFB=90°,BD=CD,进而利用△BFD≌△CDE得出即可.
(2)根据已知得出∠DEC=∠DFB=90°,BD=CD,进而利用△BFD≌△CDE得出即可.
解答:(1)解:
+1=
,
去分母得:
x-3+x-2=-3
整理得出:2x=2,
解得:x=1,
检验:当x=1时,x-2≠0,故x=1是原方程的根;
(2)证明:∵CE⊥AF,FB⊥AF,
∴∠DEC=∠DFB=90°,
又∵AD为BC边上的中线,
∴BD=CD,
∵在△BFD和△CDE中,
,
∴△BFD≌△CDE(AAS),
∴BF=CE.
| x-3 |
| x-2 |
| 3 |
| 2-x |
去分母得:
x-3+x-2=-3
整理得出:2x=2,
解得:x=1,
检验:当x=1时,x-2≠0,故x=1是原方程的根;
(2)证明:∵CE⊥AF,FB⊥AF,
∴∠DEC=∠DFB=90°,
又∵AD为BC边上的中线,
∴BD=CD,
∵在△BFD和△CDE中,
|
∴△BFD≌△CDE(AAS),
∴BF=CE.
点评:此题主要考查了分式方程的解法以及全等三角形的判定与性质,熟练掌握全等三角形的判定是解题关键.

练习册系列答案
相关题目