题目内容
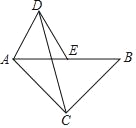
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AB=4,点E为AB的中点.以AE为边作等边△ADE(点D与点C分别在AB的异侧),连接CD.则△ACD的面积为_____.
【答案】1+![]()
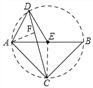
【解析】分析:根据圆的定义,证明D、A、C、B四点共圆,可得∠ADF=45°,作高线AF,构建等腰直角△ADF和30度的直角△AFC,可以求得AF、DF、CF的长,利用三角形面积公式可得结论.
详解:连接CE,
∵∠ACB=90°,E为AB的中点,
∴CE=AE=BE,
∵△ADE是等边三角形,
∴DE=AE,
∴DE=AE=CE=BE,
∴D、A、C、B在以点E为圆心的圆上,作⊙E,
∴∠ADC=∠ABC=45°,
过A作AF⊥CD于F,
∴△ADF是等腰直角三角形,
∵AD=AE=![]() AB=2,
AB=2,
∴AF=DF=![]() =
=![]() ,
,
∵∠CAF=∠DAB+∠BAC﹣∠DAF=60°+45°﹣45°=60°,
∴∠ACF=30°,
∴AC=2AF=2![]() ,
,
由勾股定理得:CF=![]() =
=![]() =
=![]() ,
,
∴S△ADC=![]() CDAF=
CDAF=![]() (
(![]() +
+![]() )×
)×![]() =1+
=1+![]() ,
,
故答案为:1![]() .
.

练习册系列答案
相关题目
【题目】为转变教育管理方式并为学校教育教学提供参考,某区240名学生参加2019年国家义务教育质量检测,在测试中随机抽取若干名学生的音乐成绩进行
某区音乐成绩分布表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
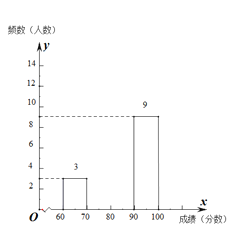
某区音乐成绩频数分布直方图
(1)频数分布表中:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)根据题意,补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,估计该区优秀学生大约有![]() 人.
人.