Question

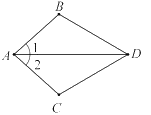
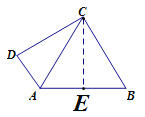
【题目】如图，四边形ABCD中， AB=10，AD=5 ，CD=12．连接AC，若AC=BC=13，则四边形ABCD的面积为_____．

Answer 1

【答案】90

【解析】

根据题意，过点C作CE⊥AB于点E，由勾股定理的逆定理，得到△ACD是直角三角形，由等腰三角形的性质得出AE=BE=AB，在Rt△CAE中根据勾股定理求出CE的长，再由S四边形ABCD=S△DAC+S△ABC即可得出结论．

解：过点C作CE⊥AB于点E，

∵AD=5 ，CD=12，AC=13，

∴，即，

∴△ACD是直角是直角三角形；

∵AC=BC=13，

∴△ABC是等腰三角形，

∵CE⊥AB，AB=10，

∴AE=BE=AB=5，

∴在Rt△ACE中，由勾股定理，得

，

∴S四边形ABCD=S△DAC+S△ABC

=

=．

故答案为：90．