题目内容
【题目】如图,抛物线y=![]() ﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
﹣x﹣4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
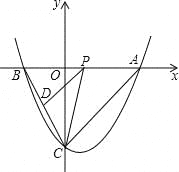
(1)直接写出A、B、C的坐标;
(2)求抛物线y=![]() ﹣x﹣4的对称轴和顶点坐标;
﹣x﹣4的对称轴和顶点坐标;
(3)求△PCD面积的最大值,并判断当△PCD的面积取最大值时,以PA、PD为邻边的平行四边形是否为菱形.
【答案】(1)A(4,0)、B(﹣2,0)、C(0,﹣4).(2)(1,﹣![]() )(3)不是菱形
)(3)不是菱形
【解析】试题分析:(1)设y=0,解一元二次方程即可求出A和B的坐标,设x=0,则可求出C的坐标.
(2)抛物线:y=![]() x2-x-4=
x2-x-4=![]() (x-1)2-
(x-1)2-![]() ,所以抛物线的对称轴是直线x=1,顶点坐标是(1,-
,所以抛物线的对称轴是直线x=1,顶点坐标是(1,-![]() ).
).
(3)设P(x,0)(-2<x<4),由PD∥AC,可得到关于PD的比例式,由此得到PD和x的关系,再求出C到PD的距离(即P到AC的距离),利用三角形的面积公式可得到S和x的函数关系,利用函数的性质即可求出三角形面积的最大值,进而得到x的值,所以PD可求,而PA≠PD,所以PA、PD为邻边的平行四边形不是菱形.
试题解析:(1)A(4,0)、B(-2,0)、C(0,-4).
(2)抛物线:y=![]() x2-x-4=
x2-x-4=![]() (x-1)2-
(x-1)2-![]() ,
,
∴抛物线的对称轴是直线x=1,顶点坐标是(1,-![]() ).
).
(3)设P(x,0)(-2<x<4),
∵PD∥AC,
∴![]() ,
,
解得:PD=![]() (x+2),
(x+2),
∵C到PD的距离(即P到AC的距离):d=PA×sin450=![]() (4-x),
(4-x),
∴△PCD的面积S=![]() ×PD×d=
×PD×d=![]() (x+2)(4-x)="-"
(x+2)(4-x)="-"![]() x2+
x2+![]() x+
x+![]() ,
,
∴S=-![]() (x-1)2+3,
(x-1)2+3,
∴△PCD面积的最大值为3,
当△PCD的面积取最大值时,x=1,PA=4-x=3,PD=![]() (x+2)=2
(x+2)=2![]() ,
,
因为PA≠PD,所以以PA、PD为邻边的平行四边形不是菱形.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案