题目内容
如图,已知A、B(-1,n)是一次函数,y=kx+b的图象与反比例函数y=| m |
| x |
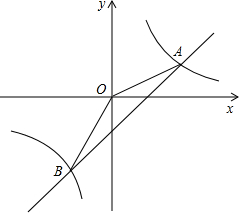 图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=
图象的两个交点,且第一象限内的点A的横坐标是它纵坐标的2倍,OA=| 5 |
(1)求点A的坐标;
(2)求反比例函数与一次函数的解析式;
(3)求△AOB的面积;
(4)求方程kx+b-
| m |
| x |
(5)求不等式kx+b-
| m |
| x |
分析:(1)首先根据A点横、纵坐标之间的关系,设出点A的坐标,利用OA的长和勾股定理来确定点A的坐标.
(2)将点A坐标代入反比例函数的解析式中,即可求得m的值,从而确定反比例函数解析式,进而可得B点的坐标,然后用待定系数法求出一次函数的解析式即可.
(3)知道了直线AB的解析式,可求得直线AB与x轴的交点(设为C)坐标,以OC为底,A、B纵坐标差的绝对值为高,可求得△AOB的面积.
(4)观察所求方程,实际求的是两个函数值相等时,x的取值,即两个函数图象交点的横坐标,在上面的解题过程中,已经求得了A、B的坐标,即可得解.
(5)此题求的是当一次函数的函数值大于反比例函数值时,x的取值范围,可结合两个函数的图象以及交点A、B的坐标来解答.
(2)将点A坐标代入反比例函数的解析式中,即可求得m的值,从而确定反比例函数解析式,进而可得B点的坐标,然后用待定系数法求出一次函数的解析式即可.
(3)知道了直线AB的解析式,可求得直线AB与x轴的交点(设为C)坐标,以OC为底,A、B纵坐标差的绝对值为高,可求得△AOB的面积.
(4)观察所求方程,实际求的是两个函数值相等时,x的取值,即两个函数图象交点的横坐标,在上面的解题过程中,已经求得了A、B的坐标,即可得解.
(5)此题求的是当一次函数的函数值大于反比例函数值时,x的取值范围,可结合两个函数的图象以及交点A、B的坐标来解答.
解答: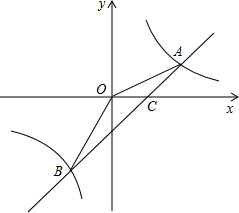 解:(1)由题意,设A(2x,x),(x>0)则有:
解:(1)由题意,设A(2x,x),(x>0)则有:
(2x)2+x2=5,解得x=1(负值舍去),
故A(2,1).
(2)由于点A位于反比例函数的图象上,则有:
m=2×1=2,即y=
;
∴B(-1,-2);
设直线AB的解析式为:y=kx+b,则有:
,解得
;
∴y=x-1;
综上可知:反比例函数的解析式为:y=
;一次函数的解析式为:y=x-1.
(3)设直线AB与x轴的交点为C,则C(1,0);
∴S△AOB=
OC•|yA-yB|=
×1×3=1.5;
即△AOB的面积为1.5平方单位.
(4)由(1)(2)知:两个函数的交点坐标为:A(2,1),B(-1,-2);
∴方程kx+b-
=0的解为:x1=2,x2=-1.
(5)由图知:当-1<x<0或x>2时,一次函数的图象在反比例函数图象的上方;
故不等式kx+b-
>0的解集为:-1<x<0或x>2.
 解:(1)由题意,设A(2x,x),(x>0)则有:
解:(1)由题意,设A(2x,x),(x>0)则有:(2x)2+x2=5,解得x=1(负值舍去),
故A(2,1).
(2)由于点A位于反比例函数的图象上,则有:
m=2×1=2,即y=
| 2 |
| x |
∴B(-1,-2);
设直线AB的解析式为:y=kx+b,则有:
|
|
∴y=x-1;
综上可知:反比例函数的解析式为:y=
| 2 |
| x |
(3)设直线AB与x轴的交点为C,则C(1,0);
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
即△AOB的面积为1.5平方单位.
(4)由(1)(2)知:两个函数的交点坐标为:A(2,1),B(-1,-2);
∴方程kx+b-
| m |
| x |
(5)由图知:当-1<x<0或x>2时,一次函数的图象在反比例函数图象的上方;
故不等式kx+b-
| m |
| x |
点评:此题主要考查了函数解析式的确定,勾股定理,图形面积的求法以及函数与方程、不等式之间的联系,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=