Question

在平面直角坐标系中，A（-1，0），B（0，2），点C在x轴上．
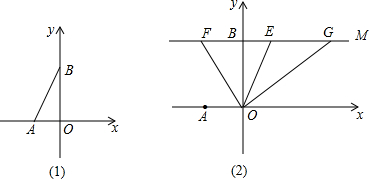
（1）如图（1），若△ABC的面积为3，则点C的坐标为

（2，0）或（-4，0）

．
（2）如图（2），过点B点作y轴的垂线BM，点E是射线BM上的一动点，∠AOE的平分线交直线BM于F，OG⊥OF且交直线BM于G，当点E在射线BM上滑动时，

∠BEO

∠BOF

的值是否变化？若不变，请求出其值；若变化，请说明理由．

Answer 1

分析：（1）利用A，B点坐标，△ABC的面积为3，得出AC的长，进而得出C点坐标；
（2）首先根据已知得出∠EOG=

1

2

∠EOx，进而得出FM∥x轴，再利用已知得出∠BOF=∠EGO，即可得出∠BEO=2∠BOF，得出答案即可．

解答：解：（1）∵A（-1，0），B（0，2），点C在x轴上．△ABC的面积为3，
∴AC的长为3，
则点C的坐标为（2，0）或（-4，0）；
故答案为：（2，0）或（-4，0）；

（2）∵∠AOE+∠EOx=180°，
∴

1

2

∠AOE+

1

2

∠EOx=90°，
即∠EOF+

1

2

∠EOx=90°
∵∠EOF+∠EOG=90°，
∴∠EOG=

1

2

∠EOx，
∴FM∥x轴，
∴∠GOx=∠EGO，
∴∠EOG=∠EGO，
∴∠BEO=2∠EGO，
∵∠FOG=90°，
∴∠EGO+∠OFG=90°，
∵FM⊥y轴，
∴∠BOF+∠OFG=90°，
∴∠BOF=∠EGO，
∴∠BEO=2∠BOF，
∴

∠BEO

∠BOF

=2．

点评：此题主要考查了三角形内角和定理应用以及平行线的判定和三角形面积求法等知识，根据已知得出FM∥x轴以及∠BOF=∠EGO是解题关键．