题目内容
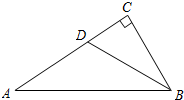
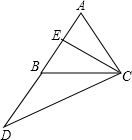
已知：如图，AB=AC=BC=BD，E是AB的中点，
求证：DC=2CE．
求证：DC=2CE．
证明：∵AB=AC=BC，
∴△ABC是等边三角形，
∴∠ABC=60°，
∵E是AB的中点，
∴CE⊥AB，
∵BC=BD，
∴∠D=∠BCD（等边对等角），
又∵∠ABC=∠D+∠BCD=60°，
∴∠D=30°，
在Rt△DCE中，DC=2CE（直角三角形30°角所对的直角边等于斜边的一半）．
∴△ABC是等边三角形，
∴∠ABC=60°，
∵E是AB的中点，
∴CE⊥AB，
∵BC=BD，
∴∠D=∠BCD（等边对等角），
又∵∠ABC=∠D+∠BCD=60°，
∴∠D=30°，
在Rt△DCE中，DC=2CE（直角三角形30°角所对的直角边等于斜边的一半）．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
