题目内容
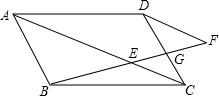
已知:如图,点E为?ABCD对角线AC上的一点,点F在BE的延长线上,且EF=BE,EF与CD相交于点G.求证:DF∥AC.
(请用两种方法证明,可以添辅助线,可以不添辅助线,如果两种方法都添辅助线,要求是不同位置的线.)
分析:证法一:连接BD,交AC于点O,由已知得BO=DO,又已知EF=BE,所以得到DF∥AC;
证法二:由已知四边形ABCD是平行四边形,所以得到AB∥CD,继而得:
=
,又由AB=CD,BE=EF,所以得:
=
,从而证得DF∥AC.
证法二:由已知四边形ABCD是平行四边形,所以得到AB∥CD,继而得:
| CG |
| AB |
| EG |
| BE |
| CG |
| CD |
| EG |
| EF |
解答: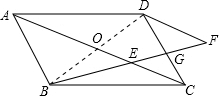 证法一:连接BD,交AC于点O.(2分)
证法一:连接BD,交AC于点O.(2分)
∵四边形ABCD是平行四边形,∴BO=DO.(2分)
∵BE=EF,∴OE∥DF,即DF∥AC.(4分)
证法二:∵四边形ABCD是平行四边形,∴AB∥CD,∴
=
.(2分)
∵AB=CD,BE=EF,∴
=
.(4分)
∴DF∥CE,即DF∥AC.(2分)
 证法一:连接BD,交AC于点O.(2分)
证法一:连接BD,交AC于点O.(2分)∵四边形ABCD是平行四边形,∴BO=DO.(2分)
∵BE=EF,∴OE∥DF,即DF∥AC.(4分)
证法二:∵四边形ABCD是平行四边形,∴AB∥CD,∴
| CG |
| AB |
| EG |
| BE |
∵AB=CD,BE=EF,∴
| CG |
| CD |
| EG |
| EF |
∴DF∥CE,即DF∥AC.(2分)
点评:此题考查的知识点平行线的性质及平行线分线段成比例,关键是由已知四边形ABCD是平行四边形,根据其性质及平行线分线段成比例证明.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 25、已知:如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,可以说明:△ACN≌△MCB,从而得到结论:AN=BM.
25、已知:如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,可以说明:△ACN≌△MCB,从而得到结论:AN=BM. 已知:如图①,点C为线段AB上一点,△ACM和△CBN都是等边三角形,AN,BM交于点P,则△BCM≌△NCA,易证结论:①BM=AN.
已知:如图①,点C为线段AB上一点,△ACM和△CBN都是等边三角形,AN,BM交于点P,则△BCM≌△NCA,易证结论:①BM=AN.
 已知:如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,
已知:如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,