题目内容
 已知:如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,
已知:如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,(1)若线段AB=a,CE=b,|a-15|+(b-4.5)2=0,求a,b;
(2)如图1,在(1)的条件下,求线段DE;
(3)如图2,若AB=15,AD=2BE,求线段CE.
分析:(1)由|a-15|+(b-4.5)2=0,根据非负数的性质即可推出a、b的值;
(2)根据(1)所推出的结论,即可推出AB和CE的长度,根据图形即可推出AC=7.5,然后由AE=AC+CE,即可推出AE的长度,由D为AE的中点,即可推出DE的长度;
(3)首先设EB=x,根据线段中点的性质推出AD、DE关于x的表达式,即AD=DE=2x,由图形推出AD+DE+BE=15,即可得方程:x+2x+2x=15,通过解方程推出x=3,即BE=3,最后由BC=7.5,即可求出CE的长度.
(2)根据(1)所推出的结论,即可推出AB和CE的长度,根据图形即可推出AC=7.5,然后由AE=AC+CE,即可推出AE的长度,由D为AE的中点,即可推出DE的长度;
(3)首先设EB=x,根据线段中点的性质推出AD、DE关于x的表达式,即AD=DE=2x,由图形推出AD+DE+BE=15,即可得方程:x+2x+2x=15,通过解方程推出x=3,即BE=3,最后由BC=7.5,即可求出CE的长度.
解答:解:(1)∵|a-15|+(b-4.5)2=0,
∴|a-15|=0,(b-4.5)2=0,
∵a、b均为非负数,
∴a=15,b=4.5,

(2)∵点C为线段AB的中点,AB=15,CE=4.5,
∴AC=
AB=7.5,
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=
AE=6,
(3)设EB=x,则AD=2BE=2x,
∵点D为线段AE的中点,
∴AD=DE=2x,
∵AB=15,
∴AD+DE+BE=15,
∴x+2x+2x=15,
解方程得:x=3,即BE=3,
∵AB=15,C为AB中点,
∴BC=
AB=7.5,
∴CE=BC-BE=7.5-3=4.5.
∴|a-15|=0,(b-4.5)2=0,
∵a、b均为非负数,
∴a=15,b=4.5,

(2)∵点C为线段AB的中点,AB=15,CE=4.5,
∴AC=
| 1 |
| 2 |
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=
| 1 |
| 2 |
(3)设EB=x,则AD=2BE=2x,
∵点D为线段AE的中点,
∴AD=DE=2x,
∵AB=15,
∴AD+DE+BE=15,
∴x+2x+2x=15,
解方程得:x=3,即BE=3,
∵AB=15,C为AB中点,
∴BC=
| 1 |
| 2 |
∴CE=BC-BE=7.5-3=4.5.
点评:本题主要考查线段中点的性质,关键在于正确的进行计算,熟练运用数形结合的思想推出相关线段之间的数量关系.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
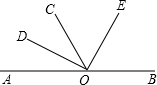 已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.