题目内容
已知:如图,点P为线段AB上的动点(与A、B两点不重合).在同一平面内,把线段AP、BP分别折成△CDP、△EFP,其中∠CDP=∠EFP=90°,且D、P、F三点共线.若△CDP、△EFP均为等腰三角形,且DF=2,求AB的长.


分析:设DP=x,PF=y,根据等腰直角三角形的性质得出CD=DP=x,EF=PF=y,再利用勾股定理分别得到PC=
x,PE=
y,进而由DF=DP+PF=x+y=2,求出AB即可.
| 2 |
| 2 |
解答:解:设DP=x,PF=y,
∵△CDP和△EFP都是等腰直角三角形,且∠CDP=∠EFP=90°,
∴CD=DP=x,EF=PE=y,
∴根据勾股定理得:CP=
=
x,PE=
=
y,
∴AB=AP+PB=CD+DP+PC+PF+EF+PE,
=x+x+
x+y+y+
y
=(2+
)(x+y),
∵DF=2,∴x+y=2.
∴AB=2(2+
)=4+2
.
∵△CDP和△EFP都是等腰直角三角形,且∠CDP=∠EFP=90°,
∴CD=DP=x,EF=PE=y,
∴根据勾股定理得:CP=
| CD2+DP2 |
| 2 |
| PF2+EF2 |
| 2 |
∴AB=AP+PB=CD+DP+PC+PF+EF+PE,
=x+x+
| 2 |
| 2 |
=(2+
| 2 |
∵DF=2,∴x+y=2.
∴AB=2(2+
| 2 |
| 2 |
点评:此题考查了等腰直角三角形的性质,以及勾股定理,利用了转化及整体的思想,熟练掌握等腰直角三角形的性质是解本题的关键.

练习册系列答案
相关题目
 26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
26、已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
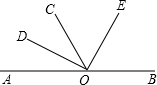 已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.
已知:如图,点O为直线AB上一点,过点O在直线AB的同侧作射线OD、OC、OE,且OD是∠AOC的平分线,∠DOE=90°,请判断OE是否是∠BOC的平分线,并说明理由.