题目内容
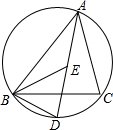（1998•江西）如图，在△ABC中，AC=BC，E是内心，AE的延长线交△ABC的外接圆于D．求证：（1）BE=AE；
（2）
| AB |
| AC |
| AE |
| DE |
分析：（1）根据等边对等角可以证得∠CAB=∠CBA，然后根据内心的定义即可证得∠1=∠3，从而依据等角对等边即可证得；
（2）首先证明△BED是等腰三角形，然后证明△ABC∽△EBD，根据相似三角形的对应边的比相等，以及（1）的结论即可证得．
（2）首先证明△BED是等腰三角形，然后证明△ABC∽△EBD，根据相似三角形的对应边的比相等，以及（1）的结论即可证得．
解答：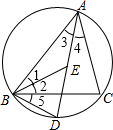
证明：（1）∵AC=BC
∴∠CAB=∠CBA，
又∵E是内心，
∴∠1=∠2=∠3=∠4．
∴BE=AE；
（2）∵∠BED=∠1+∠3，∠EDB=∠2+∠5，
又∵∠5=∠4，
∴∠BED=∠EDB，
∴BD=DE，
∴
=
，
又∵∠D=∠C
∴△ABC∽△EBD，
∴
=
，
∵BE=AE，
∴
=
．
证明：（1）∵AC=BC∴∠CAB=∠CBA，
又∵E是内心，
∴∠1=∠2=∠3=∠4．
∴BE=AE；
（2）∵∠BED=∠1+∠3，∠EDB=∠2+∠5，
又∵∠5=∠4，
∴∠BED=∠EDB，
∴BD=DE，
∴
| BD |
| BC |
| DE |
| CA |
又∵∠D=∠C
∴△ABC∽△EBD，
∴
| AB |
| AC |
| BE |
| DE |
∵BE=AE，
∴
| AB |
| AC |
| AE |
| DE |
点评：本题考查了三角形的内心的性质，以及等腰三角形的判定与性质，相似三角形的判定与性质，证明△ABC∽△EBD是关键．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
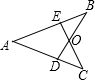（1998•江西）如图，已知AB=AC，AE=AD，那么图中全等三角形共有（ ）
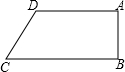（1998•江西）如图，已知直角梯形ABCD中，AD∥BC，CD=10，∠C=60°，则AB=
（1998•江西）如图，已知△ABC是边长为4的等边三角形，AB在x轴上，点C在第一象限，AC交y轴于点D，点A的坐标为（-1，0）．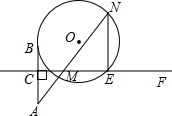
（1998•江西）如图，已知AB切⊙O于点B，AB的垂直平分线CF交AB于点C，交⊙O于D、E．设点M是射线CF上的任意一点，CM=a，连接AM，若CB=3，DE=8．