题目内容
【题目】如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，若BF=12，AB=10，则AE的长为（ ）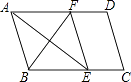 
A.13
B.14
C.15
D.16
【答案】D
【解析】解：如图所示：
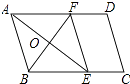
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAE=∠AEB，
∵∠BAD的平分线交BC于点E，
∴∠DAE=∠BAE，
∴∠BAE=∠BEA，
∴AB=BE，同理可得AB=AF，
∴AF=BE，
∴四边形ABEF是平行四边形，
∵AB=AF，
∴四边形ABEF是菱形，
∴AE⊥BF，OA=OE，OB=OF= 
BF=6，
∴OA= 
= 
=8，
∴AE=2OA=16；
故选：D．
先证明四边形ABEF是平行四边形，再证明邻边相等即可得出四边形ABEF是菱形，得出AE⊥BF，OA=OE，OB=OF= BF=6，由勾股定理求出OA，即可得出AE的长．
练习册系列答案
相关题目
【题目】在学校组织的科学素养竞赛中，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为90分，80分，70分，60分，学校将八年级一班和二班的成绩整理并绘制成如下的统计图：
请你根据以上提供的信息解答下列问题：
（1）此次竞赛中二班成绩在70分及其以上的人数有 人
（2）补全下表中空缺的三个统计量：
平均数（分） | 中位数（分） | 众数（分） | |
一班 | 77.6 | 80 | |
二班 | 90 |
（3）请根据上述图表对这次竞赛成绩进行分析，写出两个结论．
