题目内容
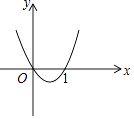
【题目】已知抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点.
(1)求m的取值范围;
(2)当m取满足条件的最大整数时,求抛物线与x轴有两个交点的坐标.
【答案】
(1)解:∵抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点,
∴y=0时,(m﹣2)x2+2mx+m+3=0,则△=(2m)2﹣4×(m﹣2)×(m+3)>0,m﹣2≠0,
解得m<6且m≠2.
即m的取值范围是:m<6且m≠2
(2)解:∵m<6且m≠2,
∴m满足条件的最大整数是m=5.
∴y=3x2+10x+8.
当y=0时,3x2+10x+8=0.
解得 ![]() .
.
即抛物线与x轴有两个交点的坐标是:(﹣2,0),( ![]() ,0)
,0)
【解析】(1)根据抛物线y=(m﹣2)x2+2mx+m+3与x轴有两个交点时,可知(m﹣2)x2+2mx+m+3=0时,△>0且m﹣2≠0,从而可以解答本题;(2)根据第一问求得的m的取值范围,可以得到m的最大整数,从而可以求得抛物线与x轴有两个交点的坐标.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.

【题目】某市射击队甲、乙两名优秀队员在相同的条件下各射耙![]() 次,每次射耙的成绩情况如图所示:
次,每次射耙的成绩情况如图所示:

![]() 请将表格补充完整:
请将表格补充完整:
平均数 | 方差 | 中位数 | 命中 | |
甲 |
|
|
| |
乙 |
|
![]() 请从下列四个不同的角度对这次测试结果进行
请从下列四个不同的角度对这次测试结果进行
①从平均数和方差向结合看,________的成绩好些;
②从平均数和中位数相结合看,________的成绩好些;
③从平均数和折线统计图走势相结合看,________的成绩好些;
④若其他队选手最好成绩在![]() 环左右,现要选一人参赛,你认为选谁参加,并说明理由.
环左右,现要选一人参赛,你认为选谁参加,并说明理由.
【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?