题目内容
 作图题:
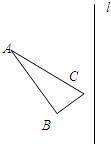
作图题:(1)如图,一个三角形状的水池,现要在水池内安装一个喷水头,且喷水头到池边的距离都要相等,请用尺规找出喷水池的位置点P.
(2)先用圆规画一个圆,然后在圆弧上确定三个点A、B、C,作线段AB、BC的垂直平分线,你能发现什么结论?
分析:(1)根据喷水头到池边的距离都相等可知,喷头应位于此三角形的内心位置,故只要作出此三角形的内心即可;
(2)根据题意画出图形,可发现两条垂直平分线的交点即为此圆的圆心.
(2)根据题意画出图形,可发现两条垂直平分线的交点即为此圆的圆心.
解答: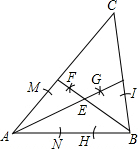 解:(1)①以A为圆心,以任意长为半径画圆分别交AC、AB于M、N两点,再分别以M、N为圆心,以大于
解:(1)①以A为圆心,以任意长为半径画圆分别交AC、AB于M、N两点,再分别以M、N为圆心,以大于
MN为半径画圆,两圆相交于G点,作射线AG,则AG即为∠A的平分线;
②同理,以B为圆心,以任意长为半径画圆分别交AB、BV于H、I两点,再分别以H、I为圆心,以大于
HI为半径画圆,两圆相交于F点,作射线BF,BF交射线AG于点E,
则E点即为所求点.
(2)两条垂直平分线的交点即为此圆的圆心.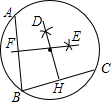
①分别以A、B为圆心,以大于
AB为半径画圆,两圆相交于E点,过点E向AB作垂线EF;
②同理,分别以B、C为圆心,以大于
BC为半径画圆,两圆相交于D点,过点D向BC作垂线DH交直线EF于点O,则O为该圆圆心.
 解:(1)①以A为圆心,以任意长为半径画圆分别交AC、AB于M、N两点,再分别以M、N为圆心,以大于
解:(1)①以A为圆心,以任意长为半径画圆分别交AC、AB于M、N两点,再分别以M、N为圆心,以大于| 1 |
| 2 |
②同理,以B为圆心,以任意长为半径画圆分别交AB、BV于H、I两点,再分别以H、I为圆心,以大于
| 1 |
| 2 |
则E点即为所求点.
(2)两条垂直平分线的交点即为此圆的圆心.

①分别以A、B为圆心,以大于
| 1 |
| 2 |
②同理,分别以B、C为圆心,以大于
| 1 |
| 2 |
点评:本题考查的是尺规作图,只要熟知角平分线及线段垂直平分线的作法即可轻松解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 18、
18、 作图题:
作图题: 作图题:
作图题: