题目内容
 作图题:
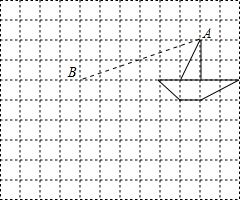
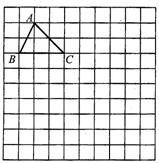
作图题:(1)如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转90°,得到△A″B″C″请你画出△A′B′C′和△A″B″C′(不要求写画法).
(2)直接写出线段的长AB=
分析:平移作图时,可先将A、B、C三点分别向下平移4个单位,得到点A′、B′、C′,再顺次连接这三点可得△A′B′C′;
旋转作图时,首先确定旋转中心:点C′,旋转方向:顺时针方向,旋转角度:90°,然后按要求作图即可.
旋转作图时,首先确定旋转中心:点C′,旋转方向:顺时针方向,旋转角度:90°,然后按要求作图即可.
解答:解:△A′B′C′和△A″B″C′如下图所示;
画法:(1)分别将点A、B、C向下平移4个单位,得到点A′、B′、C′;
(2)顺次连接A′B′、A′C′、B′C′,得△A′B′C′;
(3)以C′为旋转中心,将线段C′B′、C′A′顺时针旋转90°,得到C′A″、C′B″;
(4)连接A″B″;
结论:△A′B′C′和△A″B″C′为求作的三角形.

∵每个小正方形的边长均为1个单位,
∴AB=
,AC=2
.
故答案为:
,2
.
画法:(1)分别将点A、B、C向下平移4个单位,得到点A′、B′、C′;
(2)顺次连接A′B′、A′C′、B′C′,得△A′B′C′;
(3)以C′为旋转中心,将线段C′B′、C′A′顺时针旋转90°,得到C′A″、C′B″;
(4)连接A″B″;
结论:△A′B′C′和△A″B″C′为求作的三角形.

∵每个小正方形的边长均为1个单位,
∴AB=
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题主要考查的是平移变换和旋转变换的作图方法,在旋转作图时,一定要明确三个要素:旋转中心、旋转方向、旋转角度.

练习册系列答案
相关题目
 18、
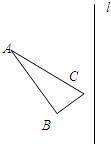
18、 作图题:
作图题: 作图题:
作图题: