题目内容
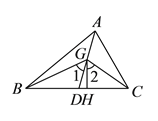
【题目】如图,ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )

A. 67.5° B. 52.5° C. 45° D. 75°
【答案】A
【解析】根据AB=AC,利用三角形内角和定理求出∠ABC的度数,再利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°,然后即可求出∠BDE的度数.
解:∵AB=AC,
∴∠ABC=∠ACB,
∵∠A=30°,
∴∠ABC=∠ACB=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵以B为圆心,BC长为半径画弧,
∴BE=BD=BC,
∴∠BDC=∠ACB=75°,
∴∠CBD=180°﹣75°﹣75°=30°,
∴∠DBE=75°﹣30°=45°,
∴∠BED=∠BDE=![]() (180°﹣45°)=67.5°.
(180°﹣45°)=67.5°.
故选C.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目