题目内容
已知PA,PB分别切⊙O于点A,B,点C在⊙O上,∠P=50°,则∠BCA的度数为( )
分析:首先根据题意画出图形,分别从点C在优弧ACB上与劣弧AB上去分析;如图1,连接OA,OB,由切线的性质与四边形内角和定理,可求得∠AOB的度数,又由圆周角定理,即可求得∠BCA的度数;如图2,连接OA,OB,在优弧上取点D,连接AD,BD,同理可得:∠ADB=65°,又由圆的内接四边形的性质,求得∠BCA的度数.
解答: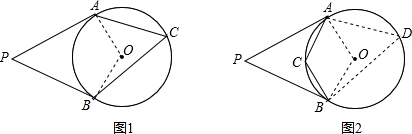 解:如图1:连接OA,OB,
解:如图1:连接OA,OB,
∵PA,PB分别切⊙O于点A,B,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠P=50°,
∴∠AOB=360°-∠P-∠OAP-∠OBP=130°,
∴∠BCA=
∠AOB=65°;
如图2,连接OA,OB,在优弧上取点D,连接AD,BD,
同理可得:∠ADB=65°,
∴∠ACB=180°-∠ADB=115°.
∴∠BCA的度数为:65°或115°.
故选D.
 解:如图1:连接OA,OB,
解:如图1:连接OA,OB,∵PA,PB分别切⊙O于点A,B,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠P=50°,
∴∠AOB=360°-∠P-∠OAP-∠OBP=130°,
∴∠BCA=
| 1 |
| 2 |
如图2,连接OA,OB,在优弧上取点D,连接AD,BD,
同理可得:∠ADB=65°,
∴∠ACB=180°-∠ADB=115°.
∴∠BCA的度数为:65°或115°.
故选D.
点评:此题考查了切线的性质、圆的内接四边形的性质以及圆周角定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
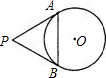 如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是( )
如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是( )| A、4 | ||
| B、8 | ||
C、4
| ||
D、8
|
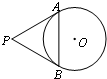 9、如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是
9、如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是 如图,已知PA,PB分别切⊙O于点A、B,⊙O的半径为2,∠P=60°,则阴影部分的面积为
如图,已知PA,PB分别切⊙O于点A、B,⊙O的半径为2,∠P=60°,则阴影部分的面积为 (2009•河西区一模)如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为
(2009•河西区一模)如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为