题目内容
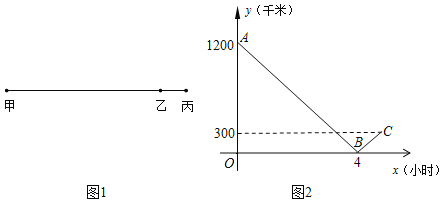
【题目】如图1所示，某乘客乘高速列车从甲地经过乙地到丙地，假设列车匀速行驶．如图2表示列车离乙地路程y（千米）与列车从甲出发后行驶时间x（小时）之间的函数关系图象．
（1）甲、丙两地间的路程为 千米；
（2）求高速列车离乙地的路程y与行驶时间x之间的函数关系式，并写出x的取值范围；
（3）当行驶时间x为多少时，高速列车离乙地的路程是200千米．
【答案】（1）1500；（2）y＝﹣300x+1200（0≤x≤4）；y＝300x﹣1200（4≤x≤5）；（3）x＝
或
．
【解析】
（1）由图可知，甲地到乙地距离1200km，乙地与丙地距离300km，进而得到甲、丙间的距离；
（2）先求出列车到达丙地的时间，然后用待定系数法分别求出从甲到乙、从乙到丙时，y与x的函数关系式；
（3）分两种情况，列出方程，即可求解．
解：（1）由函数图象可知，当x＝0时y＝1200，即刚出发时，甲与乙的距离为1200千米，
当x＝4时，y＝0，表示，4小时后列车到达乙地，故列车速度为：1200÷4＝300千米/小时，
∵300÷300＝1小时，∴1小时后列车到达丙地，乙与丙间的距离为300千米，
故甲、丙两地间的距离为：1200+3000＝1500千米，
故答案为：1500；
（2）当0≤x≤4时，设函数关系式为：y＝k1x+b1，
将（0，1200），（4，0）代入得：
，
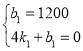解得：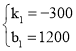
，
∴y＝﹣300x+1200；
当4≤x≤5时，设函数关系式为：y＝k2x+b2，
将（4，0），（5，300）代入得：
，
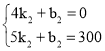解得：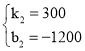
，
∴y＝300x﹣1200；
（3）①当0≤x≤4时，200＝﹣300x+1200，
∴x＝
②当4≤x≤5时，200＝300x﹣1200，
解得：x＝
综上所述：当x＝或时，高速列车离乙地的路程是200千米．
练习册系列答案
相关题目
