题目内容
【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
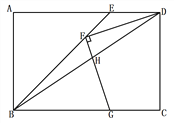
（1）如图1，在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．
（2）问题探究
小红提出了一个猜想：对角线互相平分且相等的“等邻边四边形”是正方形．她的猜想正确吗？请说明理由．
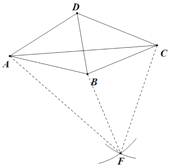
（3）如图2，“等邻边四边形”ABCD中，AB＝AD，∠BAD＋∠BCD＝90°，AC，BD为对角线，AC＝
AB．试探究线段BC，CD，BD之间的数量关系，并证明你的结论．
【答案】（1）AB＝BC，（答案不唯一），理由见解析；（2）正确；理由见解析；（3）BC2＋CD2＝2BD2，证明见解析.
【解析】试题分析：（1）利用“等邻边四边形”的定义直接判断即可，
（2）利用矩形的判定和菱形的判定和“等邻边四边形”的定义直接判断即可，
（3）先判断出△ACF∽△ABD，得到CF=
BD，再求出∠CBF=90°，最后用勾股定理即可求解.
试题解析：（1）AB＝BC，（答案不唯一）
理由：∵四边形ABCD是凸四边形，且AB＝AC，
∴四边形ABCD是“等邻边四边形”．
（2）正确；理由为：
∵四边形的对角线互相平分且相等，
∴四边形ABCD是矩形 ,
∵四边形是“等邻边四边形”，
∴这个四边形有一组邻边相等，
∴四边形ABCD是菱形 ,
∴对角线互相平分且相等的等邻边四边形是正方形；
（3）BC2＋CD2＝2BD2，证明如下：
如图，
∵AB＝AD，
∴以A为圆心，AC为半径画弧，再以B为圆心，CD为半径画弧，两弧相交于点F
则可将△ADC线绕点A旋转到△ABF，连接CF，
则△ABF≌△ADC，
∴∠ABF＝∠ADC，∠BAF＝∠DAC，AF＝AC，FB＝CD，
∴∠BAD＝∠CAF， 
，
∴△ACF∽△ABD，
∴
，
∵AC＝
AB，∴CF＝
BD，
∵∠BAD＋∠ADC＋∠BCD＋∠ABC＝360°，
∴∠ABC＋∠ADC＝360°－（∠BAD＋∠BCD）＝360°－90°＝270°,
∴∠ABC＋∠ABF＝270°，
∴∠CBF＝90°，
∴BC2＋FB2＝CF2＝(
BD)2＝2BD2，
∴BC2＋CD2＝2BD2．
