题目内容
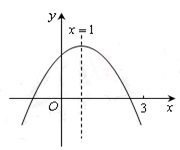
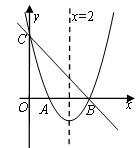
如图,直线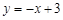 与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线
与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线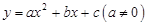 与x轴的另一交点为A,顶点为P,且对称轴是直线
与x轴的另一交点为A,顶点为P,且对称轴是直线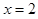 .
.
(1)求A点的坐标及该抛物线的函数表达式;
(2)求出∆PBC的面积;
(3)请问在对称轴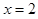 右侧的抛物线上是否存在点Q,使得以点A、B、C、Q所围成的四边形面积是∆PBC的面积的
右侧的抛物线上是否存在点Q,使得以点A、B、C、Q所围成的四边形面积是∆PBC的面积的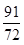 ?若存在,请求出点Q的坐标;若不存在,请说明理由.
?若存在,请求出点Q的坐标;若不存在,请说明理由.
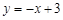 与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线
与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线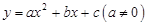 与x轴的另一交点为A,顶点为P,且对称轴是直线
与x轴的另一交点为A,顶点为P,且对称轴是直线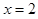 .
.(1)求A点的坐标及该抛物线的函数表达式;
(2)求出∆PBC的面积;
(3)请问在对称轴
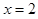 右侧的抛物线上是否存在点Q,使得以点A、B、C、Q所围成的四边形面积是∆PBC的面积的
右侧的抛物线上是否存在点Q,使得以点A、B、C、Q所围成的四边形面积是∆PBC的面积的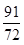 ?若存在,请求出点Q的坐标;若不存在,请说明理由.
?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)(1,0),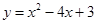 .(2)3;(3)
.(2)3;(3)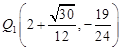 或
或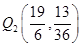
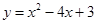 .(2)3;(3)
.(2)3;(3)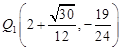 或
或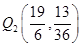
试题分析:(1)先由直线y=-x+3与x轴,y轴分别相交于点B,点C,求出B(3,0),C(0,3),再根据抛物线y=ax2+bx+c的对称轴是直线x=2,求出与x轴的另一交点A的坐标为(1,0),然后将A(1,0),B(3,0),C(0,3)代入y=ax2+bx+c,运用待定系数法即可求出该抛物线的函数表达式;
(2)先利用配方法将二次函数写成顶点式,得到顶点P的坐标,再设抛物线的对称轴交直线y=-x+3于点M,由PM∥y轴,得出M的坐标,然后根据S△PBC=
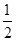 •PM•|xC-xB|即可求出△PBC的面积;
•PM•|xC-xB|即可求出△PBC的面积;(3)设Q(m,m2-4m+3),首先求出以点A、B、C、Q所围成的四边形面积=
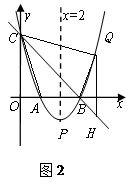
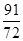 S△PBC=
S△PBC=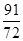 ×3=
×3=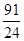 .再分两种情况进行讨论:①当点Q在PB段时,由S四边形ACBQ=S△ABC+S△ABQ=3+|yQ|,得出|yQ|=
.再分两种情况进行讨论:①当点Q在PB段时,由S四边形ACBQ=S△ABC+S△ABQ=3+|yQ|,得出|yQ|=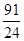 -3=
-3=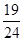 ,即-m2+4m-3=
,即-m2+4m-3=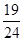 ,解方程求出m的值,得到Q1的坐标;②当点Q在BE段时,过Q点作QH⊥x轴,交直线于H,连结BQ.由S四边形ACQB=S△ABC+S△CBQ=3+
,解方程求出m的值,得到Q1的坐标;②当点Q在BE段时,过Q点作QH⊥x轴,交直线于H,连结BQ.由S四边形ACQB=S△ABC+S△CBQ=3+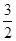 (m2-3m),得出
(m2-3m),得出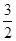 (m2-3m)=
(m2-3m)=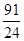 -3=
-3=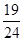 ,解方程求出m的值,得到Q2的坐标.
,解方程求出m的值,得到Q2的坐标.试题解析:(1)直线
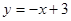 与x轴相交于点
与x轴相交于点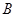 ,
,∴当
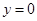 时,
时,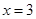 ,
,∴点
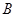 的坐标为
的坐标为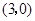 .
.又∵抛物线过
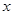 轴
轴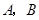 两点,且对称轴为
两点,且对称轴为 ,根据抛物线的对称性,
,根据抛物线的对称性,∴点
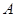 的坐标为
的坐标为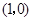 .
.∵
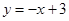 过点
过点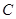 ,易知
,易知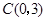 ,
,∴
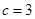 .
.又∵抛物线
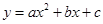 过点
过点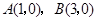 ,
,∴
 解得
解得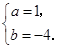
∴
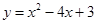 .
.(2)连结PB、PC,
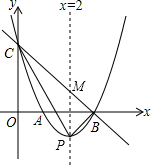
由
 ,得
,得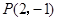 ,
,设抛物线的对称轴交直线
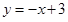 于点
于点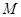 ,
,又∵PM∥y轴,则
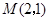 ,
,则
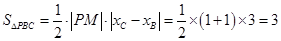
(3)由图可知,点Q应分为两种情况,在PB段或在BE段。

又
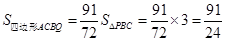
设
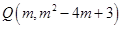
当点Q在PB段时,
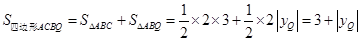 ,
,∴
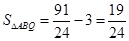 ,可知
,可知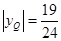
∴
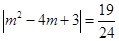 ,即
,即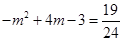 ,
,解之,得
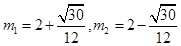 ,
,又点Q在对称轴的右侧,则
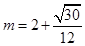 ,
,∴
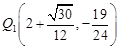
当点Q在BE段时,过Q作QH⊥x轴,交直线于H,连结BQ,则设
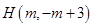
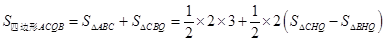 ,
,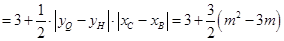
又
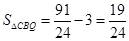 ,
,∴
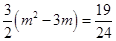 ,解之,得
,解之,得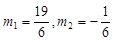
又点Q在对称轴的右侧,则
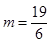 ,
,∴
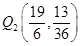
综上所述,当
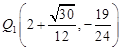 或
或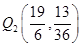 时,点A、B、C、Q所围成的四边形面积是∆PBC的面积的
时,点A、B、C、Q所围成的四边形面积是∆PBC的面积的 .
.
练习册系列答案
相关题目
 x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x=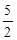 上.
上.
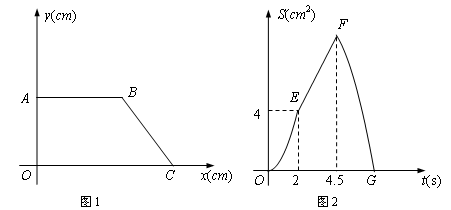
 ,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从点C出发,以1cm/s的速度沿边CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△CPQ的面积为S(cm2), 已知S与t之间的函数关系如图2中曲线段OE、线段EF与曲线段FG给出.
,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从点C出发,以1cm/s的速度沿边CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△CPQ的面积为S(cm2), 已知S与t之间的函数关系如图2中曲线段OE、线段EF与曲线段FG给出. ?
?
 与抛物线
与抛物线 的图象都经过
的图象都经过 轴上的D点,抛物线与
轴上的D点,抛物线与 轴交于A、B两点,其对称轴为直线
轴交于A、B两点,其对称轴为直线 ,且
,且 .直线
.直线 ; ②
; ② ; ③
; ③ ; ④
; ④ ; ⑤
; ⑤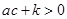


 C.2
C.2 D.2
D.2 +2
+2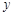 =
=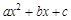 (
(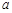 ≠0)图象如图所示,下列结论:①
≠0)图象如图所示,下列结论:①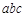 >0;②
>0;② =0;③当
=0;③当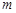 ≠1时,
≠1时, >
> ;④
;④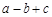 >0;⑤若
>0;⑤若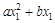 =
= ,且
,且 ≠
≠ ,则
,则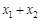 =2.其中正确的有( )
=2.其中正确的有( )