题目内容
如图,矩形OABC的两边OA、OC分别在x轴和y轴上,A(-3,0),过点C的直线y=-2x+4与x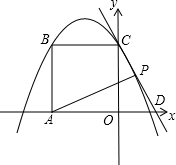 轴交于点D,二次函数y=-
轴交于点D,二次函数y=-| 1 | 2 |
(1)求B、C两点的坐标;
(2)求二次函数解析式;
(3)若点P是CD的中点,求证:AP⊥CD;
(4)在二次函数图象上是否存在点M,使以A、P、C、M为顶点的四边形为矩形?若存在,求出点M的坐标;若不存在,请说明理由.
分析:(1)令直线y=-2x+4的x=0即可得出C点坐标,再根据A、C两点坐标便可求出B点坐标;
(2)将B、C两点的坐标得到代入二次函数y=-
x2+bx+c即可求得二次函数解析式;
(3)连接AC,先证△ACD为等腰三角形,即可证明AP⊥CD
(4)存在,先证明△MNA与△COD相似,即可求得M点坐标.
(2)将B、C两点的坐标得到代入二次函数y=-
| 1 |
| 2 |
(3)连接AC,先证△ACD为等腰三角形,即可证明AP⊥CD
(4)存在,先证明△MNA与△COD相似,即可求得M点坐标.
解答:(1)解:y=-2x+4,当x=0时,y=4,∴C(0,4)
在矩形OABC中,BC=OA=3,AB=OC=4.
∴B(-3,4).
(2)解:∵二次函数y=-
x2+bx+c的图象经过B、C两点,
∴
∴
∴y=-
x2-
x+4.
(3)证明:连接AC,在Rt△AOC中,AC=
=
=5
∵y=-2x+4,当y=0时,x=2.
∴D(2,0)
∵AD=OA+OD=3+2=5.
∴AD=AC.
∵P是CD的中点,
∴AP⊥CD.
(4)解:存在,理由:假设四边形APCM为矩形,过点M作MN⊥x轴于N点,
在Rt△COD中,CD=
=
=2
.∴CP=AM=
CD=
∵MA∥CD,∴∠MAN=∠CDO.
∵∠MNA=∠COD=90°,
∴△MNA∽△COD.
∴
=
=
∴MN=4×
=2.
NA=2×
=1
∵ON=OA+AN=4
∴M(-4,2)
把x=-4代入y=-
x2-
x+4中,
y=2
∴点M在抛物线上
∴存在这样的点M,使四边形APCM为矩形.
在矩形OABC中,BC=OA=3,AB=OC=4.
∴B(-3,4).
(2)解:∵二次函数y=-
| 1 |
| 2 |
∴
|
∴
|
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
(3)证明:连接AC,在Rt△AOC中,AC=
| OA2+OC2 |
| 32+42 |

∵y=-2x+4,当y=0时,x=2.
∴D(2,0)
∵AD=OA+OD=3+2=5.
∴AD=AC.
∵P是CD的中点,
∴AP⊥CD.
(4)解:存在,理由:假设四边形APCM为矩形,过点M作MN⊥x轴于N点,
在Rt△COD中,CD=
| OC2+OD2 |
| 42+22 |
| 5 |
| 1 |
| 2 |
| 5 |
∵MA∥CD,∴∠MAN=∠CDO.
∵∠MNA=∠COD=90°,
∴△MNA∽△COD.
∴
| MN |
| CO |
| NA |
| OD |
| MA |
| CD |
∴MN=4×
| ||
2
|
NA=2×
| ||
2
|
∵ON=OA+AN=4
∴M(-4,2)
把x=-4代入y=-
| 1 |
| 2 |
| 3 |
| 2 |
y=2
∴点M在抛物线上
∴存在这样的点M,使四边形APCM为矩形.
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和等腰三角形的证明及三角形的相似等知识点,是各地中考的热点和难点,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
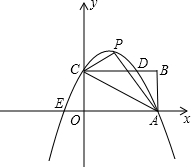 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是