题目内容
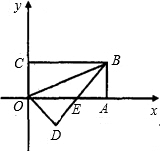 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.①求证:OE=EB;
②求OE、DE的长度;
③求直线BD的解析.
分析:①根据矩形的性质和轴对称的性质,可得∠OBC=∠BOE=∠OBE,即可证得;
②可设OE=x,则AE=DE=8-x,则在直角△EAB中,根据勾股定理,可求出x,即可解答出;
③如图,作DF⊥OE,根据直角三角形的面积,可求出DF,再根据勾股定理,可求出OF,即可得出点D的坐标,用待定系数法,即可求得直线BD的解析式.
②可设OE=x,则AE=DE=8-x,则在直角△EAB中,根据勾股定理,可求出x,即可解答出;
③如图,作DF⊥OE,根据直角三角形的面积,可求出DF,再根据勾股定理,可求出OF,即可得出点D的坐标,用待定系数法,即可求得直线BD的解析式.
解答: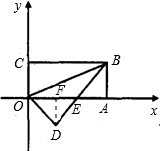 ①证明:在矩形OABC中,∠OBC=∠BOE,
①证明:在矩形OABC中,∠OBC=∠BOE,
∵△OCB≌△ODB,
∴∠CBO=∠DBO,
∴∠BOE=∠OBE,
∴OE=EB;
②解:由①可得,BD=BC=OA=8,
∴AE=DE,
设OE=BE=x,则AE=DE=8-x,
∴在直角△EAB中,(8-x)2+42=x2,
解得,x=5,则8-x=8-5=3,
∴OE=5,DE=3;
③解:如图,作DF⊥OE,垂足为F
∴在直角△ODE中,OD=4,
∴DF=
=
,
∴OF=
=
=
,
∴点D的坐标为(
,-
),
设直线BD的解析式为y=kx+b,
∴
,
解得,
,
∴直线BD的解析式为:y=
x-
.
 ①证明:在矩形OABC中,∠OBC=∠BOE,
①证明:在矩形OABC中,∠OBC=∠BOE,∵△OCB≌△ODB,
∴∠CBO=∠DBO,
∴∠BOE=∠OBE,
∴OE=EB;
②解:由①可得,BD=BC=OA=8,
∴AE=DE,
设OE=BE=x,则AE=DE=8-x,
∴在直角△EAB中,(8-x)2+42=x2,
解得,x=5,则8-x=8-5=3,
∴OE=5,DE=3;
③解:如图,作DF⊥OE,垂足为F
∴在直角△ODE中,OD=4,
∴DF=
| 3×4 |
| 5 |
| 12 |
| 5 |
∴OF=
| OD2-DF2 |
42-(
|
| 16 |
| 5 |
∴点D的坐标为(
| 16 |
| 5 |
| 12 |
| 5 |
设直线BD的解析式为y=kx+b,
∴
|
解得,
|
∴直线BD的解析式为:y=
| 4 |
| 3 |
| 20 |
| 3 |
点评:本题主要考查了矩形的性质、轴对称图形的性质、勾股定理和一次函数解析式的求法,本题涉及的知识点比较多,考查了学生对于知识的综合运用能力.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
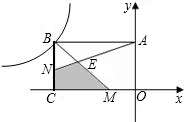
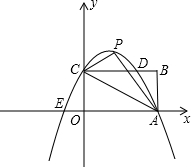 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA=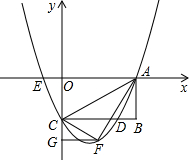 (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2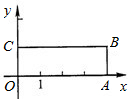 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是