题目内容
如图,矩形OABC的边OA、OC在坐标轴上,经过点B的双曲线的解析式为y=| k |
| x |
| 13 |
| 4 |

分析:此题可先设出矩形ABCO的面积为S,再将阴影面积进行分割求得阴影面积与S的关系求得S的值,则|k|=S且k<0可求得k的值.
解答: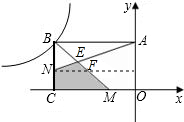 解:设矩形ABCO的面积为S,过点N作AB的平行线交BM于点F.
解:设矩形ABCO的面积为S,过点N作AB的平行线交BM于点F.
由于CM=2OM,N为BC的中点,则NF=
CM=
×
AB=
AB,
所以
=
,S△BEN=
S△ABN=
S矩形ABCO=
S.
S四边形EMCN=S△BCM-S△BNE=
S-
S=
.
解得:S=12,
则|k|=12,又由于k<0,所以k=-12.
故答案为:-12.
 解:设矩形ABCO的面积为S,过点N作AB的平行线交BM于点F.
解:设矩形ABCO的面积为S,过点N作AB的平行线交BM于点F.由于CM=2OM,N为BC的中点,则NF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
所以
| NE |
| AN |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 16 |
S四边形EMCN=S△BCM-S△BNE=
| 1 |
| 3 |
| 1 |
| 16 |
| 13 |
| 4 |
解得:S=12,
则|k|=12,又由于k<0,所以k=-12.
故答案为:-12.
点评:本题借助图形考查了反比例函数系数k的几何意义,由阴影图形的面积得到|k|的值是本题的解题思路,有一定的难度.

练习册系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.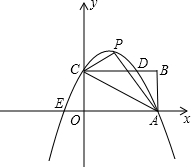 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是